Sliding-Mode Observer Based Voltage-Sensorless Model Predictive Power Control of PWM Rectifier Under Unbalanced Grid Condition

ABSTRACT:

A sliding-mode grid voltage observer (SMGVO) is proposed and experimentally verified in this paper for voltage-sensorless operation under an unbalanced network. Fundamental positive sequence component (FPSC) and fundamental negative sequence component (FNSC) are inherently separated in the observer without employing any additional filters. Due to embedded filtering effect, high frequency chattering and harmonic ripples can be well suppressed. Additionally, DC component can be completely rejected. As a result, DC offset would not cause fundamental frequency oscillations in magnitude and frequency of the estimated FPSC and FNSC. Owing to the predictive ability of SMGVO, one-step delay can be directly compensated using state variables in the observer. By combining estimation and prediction into one stage, the designed SMGVO turns out to be a compact solution for finite control set-model predictive power control (FCS-MPPC) without voltage sensors. Theoretical proof is derived to verify that FPSC and FNSC can be accurately estimated and separated. Experimental results obtained from a two-level PWM rectifier confirm the effectiveness of the whole control system.

KEYWORDS:

1.      Predictive power control

2.      Unbalanced grid

3.      Voltage observer

4.      Voltage sensorless

SOFTWARE: MATLAB/SIMULINK

BLOCK DIAGRAM:

Fig. 1. Control diagram of SMGVO based FCS-MPPC.

 EXPECTED SIMULATION RESULTS:

Fig. 2. Startup responses with 50% voltage dip in phase A. (a) Actual grid voltages, currents and estimated voltages; (b) comparison between estimated voltages from SMGVO and calculated voltages from DSOGI.

Fig. 3. Operation from balanced condition to unbalanced condition. (a) Actual grid voltages, currents and estimated voltages; (b) comparison with usogi p and usogi n calculated from actual voltage by DSOGI.

Fig. 4. Dynamic responses when Pref steps from 600 W to 1000 W.

Fig. 5. Steady state responses with 1.5 V DC component and 50% AC voltage dip in phase A.

Fig. 6. Average switching frequency fsw when Pref = 1 kW.

Fig. 7. Spectrum analysis of (a) grid voltage, (b) ^up and (b) ^un under unbalanced and distorted grid conditions.

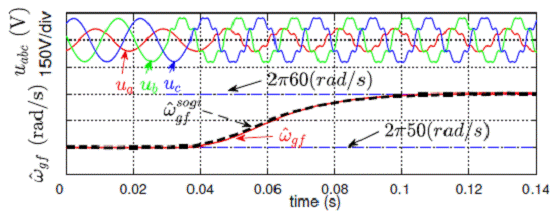
Fig. 8. Estimated grid frequency with sudden frequency step change of +10 Hz under unbalanced and distorted grid conditions.

CONCLUSION:

A SMGVO is designed and experimentally verified in this paper. It has the following properties: 1) inherent separation of FPSC and FNSC without utilizing any filters; 2) no high frequency chattering; 3) satisfactory DC component rejection; 4) comparable performance with DSOGI based sequence separation using measured voltage; 5) predictive ability to compensate one-step delay in predictive control. FCS-MPPC is implemented based on SMGVO and tested on a two-level PWM rectifier to verify the effectiveness of the control system. Experimental results show that FPSC and FNSC can be accurately estimated and separated. The dynamic performance of SMGVO during voltage sag is similar to that of DSOGI. The implemented voltage sensorless FCSMPPC presents fast dynamic responses which can track power reference quickly. Direct start without initial knowledge of grid voltage is possible due to fast converging rate of SMGVO and high regulation bandwidth of FCS-MPPC.

REFERENCES:

[1] Z. Zhang, H. Xu, M. Xue, Z. Chen, T. Sun, R. Kennel, and C. M. Hackl, “Predictive control with novel virtual-flux estimation for backto- back power converters,” IEEE Trans. Ind. Electron., vol. 62, no. 5, pp. 2823–2834, May 2015.

[2] A. M. Razali, M. A. Rahman, G. George, and N. A. Rahim, “Analysis and design of new switching lookup table for virtual flux direct power control of grid-connected three-phase PWM AC - DC converter,” IEEE Trans. Ind. Appl., vol. 51, no. 2, pp. 1189–1200, March 2015.

[3] J. Kukkola and M. Hinkkanen, “State observer for grid-voltage sensorless control of a converter equipped with an LCL filter: Direct discretetime design,” IEEE Trans. Ind. Appl., vol. 52, no. 4, pp. 3133–3145, July 2016.

[4] H.-S. Song, I.-W. Joo, and K. Nam, “Source voltage sensorless estimation scheme for PWM rectifiers under unbalanced conditions,” IEEE Trans. Ind. Electron., vol. 50, no. 6, pp. 1238–1245, Dec 2003.

[5] K. H. Ahmed, A. M. Massoud, S. J. Finney, and B. W. Williams, “Sensorless current control of three-phase inverter-based distributed generation,” IEEE Trans. Power Del., vol. 24, no. 2, pp. 919–929, April 2009.

Grid Voltages Estimation for Three-Phase PWM Rectifiers Control Without AC Voltage Sensors

 ABSTRACT

This paper proposes a new AC voltage sensorless control scheme for three-phase pulse-width modulation rectifier. A new startup process to ensure a smooth starting of the system is also proposed. The sensorless control scheme uses an adaptive neural (AN) estimator inserted in voltage-oriented control to eliminate the grid voltage sensors. The developed AN estimator combines an adaptive neural network in series with an adaptive neural filter. The AN estimator structure leads to simple, accurate and fast grid voltages estimation, and makes it ideal for low cost digital signal processor implementation. Lyapunov based stability and parameters tuning of the AN estimator are performed. Simulation and experimental tests are carried out to verify the feasibility and effectiveness of the AN estimator. Obtained results show that; the proposed AN estimator presented faster convergence and better accuracy than the second order generalized integrator based estimator; the new startup procedure avoided the over-current and reduced the settling time; the AN estimator presented high performances even under distorted and unbalanced grid voltages.

KEYWORDS

1.      AC voltage sensorless control

2.      Adaptive neural (AN) estimator

3.      Grid voltages estimation

4.      Neural networks (NNs)

5.      Pulse-width modulation (PWM) rectifier

6.       Startup process

7.      Voltage-oriented control (VOC)

SOFTWARE:  MATLAB/SIMULINK

BLOCK DIAGRAM:

Fig. 1. Overall structure of the developed AC voltage sensorless control.

EXPECTED SIMULATION RESULTS

Fig. 2. Steady-state performances of the AN estimator in diode rectifier operation mode (experiment): (a) computed input voltages vαn and vβn, (b) actual AC-line currents iα and iβ, (c) actual grid voltage eα, estimated grid voltage eα,est and estimation error and (d) actual grid voltage eβ, estimated grid voltage eβ,est and estimation error.

Fig. 3. Steady-state performances of the PLL in diode rectifier operation mode (experiment): (a) computed dq components (ed, eq) with actual grid  voltages and computed dq components (ed,est, eq,est) with estimated grid  voltages and (b) computed angles θ and θest with actual and estimated grid voltages, respectively.

Fig. 4. Performances of the AN estimator at startup (experiment): (a) input voltages vαn and vβn, (b) actual AC-line currents iα and iβ, (c) reference and  measured DC-link voltages (Vdc ref, Vdc), (d) actual grid voltage eα, estimated  grid voltage eα,est and estimation error and (d) actual grid voltage eβ, estimated grid voltage eβ,est and estimation error.

Fig. 5. Performances of the PLL at startup (experiment): (a) computed dq components (ed, eq) with actual grid voltages and computed dq components (ed,est, eq,est) with estimated grid voltages and (b) computed angles θ and θest with actual and estimated grid voltages, respectively.

Fig. 6. Transient performances of the AN estimator under Vdc ref step change (experiment): (a) actual grid voltage eα, estimated grid voltage eα,est and estimation error, (b) actual grid voltage eβ, estimated grid voltage eβ,est and estimation error, (c) actual AC-line currents iα and iβ and (d) reference and measured DC-link voltages.

Fig. 7. Transient performances of the PLL under Vdc ref step change (experiment): (a) computed dq components (ed, eq) with actual grid voltages and computed dq components (ed,est, eq,est) with estimated grid voltages and (b) computed angles θ and θest with actual and estimated grid voltages, respectively.

Fig. 8. Transient performances of the AN estimator under load resistance variation (experiment): (a) actual grid voltage eα, estimated grid voltage eα,est and estimation error, (b) actual grid voltage eβ, estimated grid voltage eβ,est and estimation error and (c) actual AC-line currents.

Fig. 9. Transient performances of the PLL under load resistance variation (experiment): (a) computed dq components (ed, eq) with actual grid voltages and computed dq components (ed,est, eq,est) with estimated grid voltages and (b) computed angles θ and θest with actual and estimated grid voltages, respectively.

Fig. 10. Transient performances of the AN estimator under symmetric grid voltages sag (experiment): (a) actual grid voltage eα, estimated grid voltage eα,est and estimation error and (b) actual grid voltage eβ, estimated grid voltage eβ,est and estimation error and (c) actual AC-line currents.

Fig. 11. Transient performances of the PLL under symmetric grid voltages sag (experiment): (a) computed dq components (ed, eq) with actual grid voltages and computed dq components (ed,est, eq,est) with estimated grid voltages and (b) computed angles θ and θest with actual and estimated grid voltages, respectively.

Fig. 12. Transient performances of the AN estimator under grid voltages unbalance (experiment): (a) actual grid voltage eα, estimated grid voltage eα,est and estimation error and (b) actual grid voltage eβ, estimated grid voltage eβ,est and estimation error and (c) actual AC-line currents.

Fig. 13. Transient performances of the PLL under grid voltages unbalance (experiment): computed dq components (ed, eq) with actual grid voltages and computed dq components (ed,est, eq,est) with estimated grid voltages and (b) computed angles θ and θest with actual and estimated grid voltages, respectively.

Fig. 14. Transient performances of the AN estimator under distorted grid voltages (simulation): (a) actual grid voltage eα and estimated grid voltage eα,est, (b) actual grid voltage eβ and estimated grid voltage eβ,est and (c) actual AC-line currents.

Fig. 15. Transient performances of the PLL under distorted grid voltages (simulation): computed dq components (ed, eq) with actual grid voltages and computed dq components (ed,est, eq,est) with estimated grid voltages and (b) computed angles θ and θest with actual and estimated grid voltages respectively.

CONCLUSION

In this work, a new AN estimator for eliminating the grid voltage sensors in VOC of three-phase PWM rectifier has been proposed. The developed AN estimator combines estimation capability of the ANN and filtering property of the ANF. Lyapunov’s theory based stability analysis has been exploited for optimal tuning of the AN estimator. Hence, simple, accurate and fast grid voltages estimation has been obtained. To avoid current overshoot and to reduce the settling time at the startup, a new startup process has been proposed to initialize the VOC. The effectiveness of the proposed procedure has been experimentally demonstrated. A comparison between the proposed AN estimator and the recently developed SOGI based estimator has been conducted. This comparison has clearly indicated faster convergence and better accuracy of the proposed estimator. Finally, robustness of the AN estimator regarding to step change in DC-link voltage reference, load resistance variation and non-ideal grid voltages conditions (symmetrical sag, unbalance, distortion) has been investigated through simulation and experimental tests. The obtained results have demonstrated high performances of the proposed AN estimator within the analyzed working conditions.

REFERENCES

[1] R. Teodorescu, M. Liserre, and P. Rodriguez, Grid converters for photovoltaic and wind power systems, John Wiley & Sons, 2011.

[2] A.-R. Haitham, M. Malinowski, and K. Al-Haddad, Power electronics for renewable energy systems, transportation and industrial applications, John Wiley & Sons, 2014.

[3] T. Friedli, M. Hartmann, and J. W. Kolar, “The essence of three-phase PFC rectifier systems–Parte II,” IEEE Trans. Power Electron., vol. 29, no. 2, pp. 543–560, Feb. 2014.

[4] M. B. Ketzer and C. B. Jacobina, “Sensorless control technique for PWM rectifiers with voltage disturbance rejection and adaptive power factor,” IEEE Trans. Ind. Electron., vol. 62, no. 2, pp. 1140–1151, Feb. 2015.

[5] A. Bechouche, H. Seddiki, D. Ould Abdeslam, and K. Mesbah, “Adaptive AC filter parameters identification for voltage-oriented control of three-phase voltage-source rectifiers”, Int. J. Modell. Identification Control, vol. 24, no. 4, pp. 319–331, 2015.

Direct Power Control of Pulse Width Modulated Rectifiers without DC Voltage Oscillations under Unbalanced Grid Conditions

ABSTRACT:

Direct power control with space vector modulation (DPC-SVM) features simple structure, fast dynamic performance and little tuning work. However, conventional DPC-SVM can not achieve accurate power control under unbalanced grid conditions. A modified DPC-SVM is thus proposed for accurate power control under both ideal and unbalanced grid conditions. Though power control accuracy is improved when compared with conventional DPCSVM, it still suffers highly distorted grid current and DC voltage oscillations with an unbalanced network. Therefore, a power compensation method is subsequently derived aiming at the following targets: eliminating DC voltage oscillations, achieving sinusoidal grid current and obtaining unity power factor. To that end, average grid-side reactive power and oscillations in converter-side active power are controlled as zero by simply adding a compensation to original power reference. Additionally, the proposed method does not require extraction of positive sequence or negative sequence component of grid voltage. Compared with conventional DPC-SVM in ideal grid, only additional compensation of power reference is required. As a result, control performance can be significantly improved without substantial increase of complexity. The superiority of the proposed method over the prior DPC-SVM is validated by both simulation and experimental results obtained on a two-level PWM voltage source rectifier.

KEYWORDS:

1.      Predictive power control

2.      Power compensation

3.      Unbalanced grid

SOFTWARE: MATLAB/SIMULINK

BLOCK DIAGRAM:

Fig. 1. Control diagram of the proposed DPC-SVM.

EXPECTED SIMULATION RESULTS:

Fig. 2. Simulation results of Uabc, Pin, Pref , Qin, Qref and Iabc for (a) the MDPC-SVM and (b) CDPC-SVM.

Fig. 3. Simulation results of Uabc, Pin, Pref , Pout, Udc and Iabc for (a) MDPC-SVM-PC and (b) MDPC-SVM

Fig. 4. Simulation results of MDPC-SVM-PC when 50% voltage dip in phase A is suddenly applied.

Fig. 5. Simulation results of MDPC-SVM-PC when both R and L in the controller are (a) 50% and (b) 150% of their actual value.

Fig. 6. Simulated results of MDPC-SVM-PC under one phase grounding fault.

CONCLUSION:

In existing literature, most studies on DPC-SVM were carried out under balanced grid voltage conditions. Under unbalanced grid voltage conditions, the steady-state performance of DPC-SVM are seriously deteriorated by exhibiting highly distorted current and oscillations in the DC-link voltage. To cope with these problems, this paper proposes a novel DPC-SVM method, which is able to work effectively under both balanced and unbalanced grid conditions. An appropriate power compensation is derived, which only requires the grid/converter voltages and their delayed values. By adding this power compensation to the original power references without modifying the internal control structure, constant DC-link voltage and sinusoidal grid currents are achieved simultaneously without affecting the average value of gridside active power and reactive power. The proposed DPC-SVM is compared to conventional DPC-SVM and its effectiveness is confirmed by the presented simulation and experimental results.

Due to additional calculation of power compensation, complexity of the proposed DPC-SVM is higher than conventional power control schemes. However, twice grid voltage frequency oscillations can be completely eliminated in theory by the proposed method under unbalanced grid conditions, which is beneficial to the lifetime and maintenance of capacitors. Although using a larger capacitor can also reduce DC voltage ripples, it may increase hardware cost and volume of the system. In this sense, the proposed method is more suitable for the application where a high quality DC voltage is required under unbalanced grid conditions.

REFERENCES:

[1] Z. Zhang, H. Fang, F. Gao, J. Rodríguez, and R. Kennel, “Multiplevector model predictive power control for grid-tied wind turbine system with enhanced steady-state control performance,” IEEE Trans. Ind. Electron., vol. 64, DOI 10.1109/TIE.2017.2682000, no. 8, pp. 6287– 6298, Aug. 2017.

[2] A. Koran, T. LaBella, and J. S. Lai, “High efficiency photovoltaic source simulator with fast response time for solar power conditioning systems evaluation,” IEEE Trans. Power Electron., vol. 29, DOI 10.1109/TPEL.2013.2262297, no. 3, pp. 1285–1297, Mar. 2014.

[3] A. Camacho, M. Castilla, J. Miret, A. Borrell, and L. G. de Vicuña, “Active and reactive power strategies with peak current limitation for distributed generation inverters during unbalanced grid faults,” IEEE Trans. Ind. Electron., vol. 62, DOI 10.1109/TIE.2014.2347266, no. 3, pp. 1515–1525, Mar. 2015.

[4] W. Jiang, Y. Wang, J. Wang, L. Wang, and H. Huang, “Maximizing instantaneous active power capability for pwm rectifier under unbalanced grid voltage dips considering the limitation of phase current,” IEEE Trans. Ind. Electron., vol. 63, DOI 10.1109/TIE.2016.2577544, no. 10, pp. 5998–6009, Oct. 2016.

[5] H. Yang, Y. Zhang, J. Liang, J. Gao, P. Walker, and N. Zhang, “Sliding mode observer based voltage-sensorless model predictive power control of pwm rectifier under unbalanced grid condition,” IEEE Trans. Ind. Electron., vol. PP, DOI 10.1109/TIE.2017.2774730, no. 99, pp. 1–1, 2017.