Impacts of Grid Voltage Harmonics Amplitude and Phase Angle Values on Power Converters in Distribution Networks

ABSTRACT:

Motor drive systems based on diode-rectifier are utilised in many industrial and commercial applications due to their cost-effectiveness and simple topology. However, these diode rectifier-based systems can be affected by power quality and harmonics in distribution networks. Thus, this paper investigates the impact of grid voltage harmonics on the operation of power converters with three-phase diode rectifier using mathematical formulation of the drive voltage and current harmonics based on grid voltage harmonics. Simulation analysis and practical tests have been then carried out to validate the mathematical equations and the impact of grid voltage harmonics on the power converter harmonics. The results illustrate that even a small amount of grid voltage harmonics (around 4%) could significantly impact the input current harmonic contents of the three-phase diode rectifier. It is also shown that the phase-angle of grid voltage harmonics plays a crucial role to improve or deteriorate the input current harmonics of the power converters. In the next step, the optimum condition of grid voltage harmonics to minimise the input current harmonics has been evaluated and verified based on different grid codes. Finally, a harmonic mitigation technique in multi-drive systems using Electronic Inductor is proposed to mitigate the current harmonics at the PCC.

KEYWORDS:

1.      Distorted grid

2.      Distribution networks

3.      Total harmonic distortion

4.      Three-phase rectifier

  Voltage harmonics

SOFTWARE: MATLAB/SIMULINK

CIRCUIT DIAGRAM:

Figure 1. Simulink Model For The Tested Asd Under The Presence Of Voltage Harmonics At The Pcc.

 EXPECTED SIMULATION RESULTS:

 

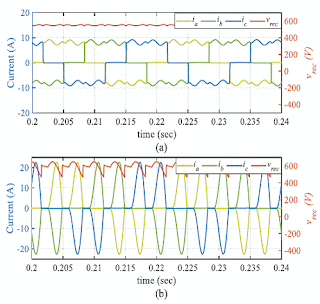
Figure 2. Simulation Results Of The Three-Phase Input Currents And Vrec

In Case: (A) 1, (B) 2, And (C) 3.

Figure 3. Practical Measurements Of The Three-Phase Input Currents And Vrec In Cases: (A) 1, (B) 2, And (C) 3.

 

Figure 4. Simulation Results Of The Three-Phase Input Currents And Vrec

In Cases: (A) Ieee-Min, (B) Ieee-Max.

Figure 5. Practical Measurements Of The Three-Phase Input Currents

And Vrec In Cases: (A) Ieee-Min, (B) Ieee-Max.

Figure 6. Simulation Results For Phase ``A'' Current When U1 Mitigates

Harmonics Generated By U2: (A) Case 3, (B) Ieee-Max Case.

 

Figure 7. Simulation Results For Output Voltage (Vo), Inductor Current, And Phase ``A'' Inverter Side Current Of U1.

CONCLUSION:

 

In this paper, the impact of grid voltage distortion on power converter current harmonics emission has been investigated. For that aim, ASDs with conventional diode rectifier has been considered to represent the power electronic system. A mathematical formulation of the rectified voltage, inductor current, and input currents of a three-phase diode rectifier is derived under the presence of voltage harmonics at the PCC. Different cases of voltage harmonics are then considered in the analysis to investigate the behaviour of the rectified voltage and the input current harmonics. The results show that the presence of even a small level of voltage harmonics (4%) at the PCC can change the current THDi by up to 30%. Furthermore, it has been shown that the phase-angle of the voltage harmonics can have a significant impact on the input current harmonics. Depending on the voltage harmonic phase-angle, the same amount of voltage harmonics could improve or deteriorate the rectified voltage ripple and the input current THDi. Moreover, the voltage harmonic phase-angle could create a phase delay (1) in the diodes conduction time. A positive 1 impacts the displacement power factor negatively, whereas a negative 1 improves that factor. Finally, a harmonic mitigation technique to compensate the high level of current harmonics using Electronic Inductor (EI) is presented.

REFERENCES:

[1] B. K. Bose, ``Power electronics and motor drives recent progress and perspective,'' IEEE Trans. Ind. Electron., vol. 56, no. 2, pp. 581_588, Feb. 2009.

[2] B. K. Bose, ``Energy, environment, and advances in power electronics,'' IEEE Trans. Power Electron., vol. 15, no. 4, pp. 688_701, Jul. 2000.

[3] W. Gray and F. Haydock, ``Industrial power quality considerations when installing adjustable speed drive systems,'' in Proc. IEEE Cement Ind. Tech. Conf. XXXVII Conf. Rec., San Juan, PR, USA, Jun. 1995, pp. 17_33.

[4] P. Waide and C. U. Brunner, ``Energy-ef_ciency policy opportunities for electric motor-driven systems,'' Int. Energy Agency, Paris, France, Work. Paper, 2011, pp. 1_128.

[5] B. Singh, B. N. Singh, A. Chandra, K. Al-Haddad, A. Pandey, and D. P. Kothari, ``A review of three-phase improved power quality AC-DC converters,'' IEEE Trans. Ind. Electron., vol. 51, no. 3, pp. 641_660, Jun. 2004.

Hybrid Wind/PV/Battery Energy Management-Based Intelligent Non-Integer Control for Smart DC-Microgrid of Smart University

ABSTRACT:

 Global environmental changes, nuclear power risks, losses in the electricity grid, and rising energy costs are increasing the desire to rely on more renewable energy for electricity generation. Recently, most people prefer to live and work in smart places like smart cities and smart universities which integrating smart grid systems. The large part of these smart grid systems is based on hybrid energy sources which make the energy management a challenging task. Thus, the design of an intelligent energy management controller is required. The present paper proposes an intelligent energy management controller based on combined fuzzy logic and fractional-order proportional-integral-derivative (FO-PID) controller methods for a smart DC-microgrid. The hybrid energy sources integrated into the DC-microgrid are constituted by a battery bank, wind energy, and photovoltaic (PV) energy source. The source-side converters (SSCs) are controller by the new intelligent fractional order PID strategy to extract the maximum power from the renewable energy sources (wind and PV) and improve the power quality supplied to the DC-microgrid. To make the microgrid as cost-effective, the (wind and PV) energy sources are prioritized. The proposed controller ensures smooth output power and service continuity. Simulation results of the proposed control schema under Matlab/Simulink are presented and compared with the super twisting fractional-order controller.

KEYWORDS:

1.      Renewable energy

2.      Smart university

3.      DC-microgrid

4.      Energy management control

5.      Fuzzy logic control

6.      Fractional order control

SOFTWARE: MATLAB/SIMULINK

SCHEMATIC DIAGRAM:

 

 

Figure 1. Studied Hybrid System Structure.

EXPECTED SIMULATION RESULTS:

Figure 2. Wind Speed.

Figure 3. Wind Power.

Figure 4. Solar Power.

Figure 5. Sscs Power.

Figure 6. Bss Power.

Figure 7. The Battery Soc.

Figure 8. Dc-Link Voltage.

Figure 9. Load Power.

Figure 10. Load Voltage.

Figure 11. Random Wind Speed.

 

CONCLUSION:

In this paper, a novel intelligent fractional order PID controller is proposed for the Energy management of hybrid energy sources contacted to a smart grid through a DC-link voltage. The hybrid energy sources integrated to the DC-microgrid are constituted by a battery bank, wind energy, and photovoltaic (PV) energy source. The source side converters (SCCs) are controller by the new intelligent fractional order PID strategy to extract the maximum power from the renewable energy sources (wind and PV) and improve the power quality supplied to the DC-microgrid. To make the microgrid as cost-effective, the (Wind and PV) energy sources are prioritized. The proposed controller ensures smooth output power and service continuity. Simulation results of the proposed control schema under Matlab/Simulink are presented and compared with the other nonlinear controls. Extensive comparative analysis with super twisting fractional order control, FO-PID and PID is demonstrated in Table 3, where it can be seen that the proposed strategy generates more power and show high performance over the proposed control strategies. From the present comparative analysis, the proposed controller producesC3.15% wind power,C50% PV power,C2.5% load power over the super twisting fractional-order and more when compared to the PID control. Future works will be focused on the experimental validation of the proposed control with a real test bench.

REFERENCES:

[1] H. T. Dinh, J. Yun, D. M. Kim, K. Lee, and D. Kim, ``A home energy management system with renewable energy and energy storage utilizing main grid and electricity selling,'' IEEE Access, vol. 8, pp. 49436_49450, 2020.

[2] C. Byers and A. Botterud, ``Additional capacity value from synergy of variable renewable energy and energy storage,'' IEEE Trans. Sustain. Energy, vol. 11, no. 2, pp. 1106_1109, Apr. 2020.

[3] M. Rizwan, L. Hong, W. Muhammad, S. W. Azeem, and Y. Li, ``Hybrid Harris Hawks optimizer for integration of renewable energy sources considering stochastic behavior of energy sources,'' Int. Trans. Elect. Energy Syst., vol. 31, no. 2, 2021, Art. no. e12694, doi: 10.1002/2050- 7038.12694.

[4] Y. Sun, Z. Zhao, M. Yang, D. Jia,W. Pei, and B. Xu, ``Overview of energy storage in renewable energy power _uctuation mitigation,'' CSEE J. Power Energy Syst., vol. 6, no. 1, pp. 160_173, 2020.

[5] T. Salameh, M. A. Abdelkareem, A. G. Olabi, E. T. Sayed, M. Al-Chaderchi, and H. Rezk, ``Integrated standalone hybrid solar PV, fuel cell and diesel generator power system for battery or supercapacitor storage systems in khorfakkan, united arab emirates,'' Int. J. Hydrogen Energy, vol. 46, no. 8, pp. 6014_6027, Jan. 2021.

High Order Disturbance Observer Based PI-PI Control System With Tracking Anti-Windup Technique for Improvement of Transient Performance of PMSM

ABSTRACT:

This paper focuses on designing a disturbance observer-based control (DOBC) system for PMSM drives. The cascade structure of the discrete-time PI-PI control system with tracking anti-windup scheme has been designed for both loops. In this study, high order disturbance observer (HODO) based control is used to improve the speed tracking performance of the control system for the PMSM prototyping kit regardless of the disturbance and unmodelled dynamics. The motion equation was modified in the HODO in which torque losses due to the drug resulting from the time-varying flux, hysteresis, and friction have been taken into account to estimate the total disturbance. The HODO does not require the derivatives of the disturbance to be zero, like in the traditional ones. It demonstrates its ability to estimate along with a load torque the high order disturbances caused by a cogging torque and a high-frequency electromagnetic noise in the PMSM system. In the real-time experiments, the proposed algorithm with HODO achieves less speed errors and faster response comparing with the baseline controller. The performances with proposed and baseline control have been evaluated under mechanical speed and load torque variation cases. The experimental results have proved the feasibility of the proposed control scheme. The proposed disturbance observer-based control system was implemented with a Lucas-Nuelle 300 W PMSM prototyping kit.

KEYWORDS:

1.      Disturbance observer based control

2.      High-order disturbance observer

3.      PI controller

4.      PMSM

      Cascaded PI-PI

      Load torque observer

SOFTWARE: MATLAB/SIMULINK

BLOCK DIAGRAM:

Figure 1. Proposed Dobc Based Control Method Structure.

 EXPECTED SIMULATION RESULTS:

Figure 2. Experimental Results Of The Proposed Hodo Based Pi With Novel Anti-Windup Scheme For Case 1. (A) Mechanical Speed Response Of Pmsm; (B) Mechanical Speed Error; (C) Estimated Load Torque Disturbance.

 

Figure 3. Dq-Axis Currents Of The Proposed Hodo Based Pi With Novel Anti-Windup Scheme For Case 1. (A)Ids And Its Desired Value Idsd; (B) Iqs And Its Desired Value Iqsd

 

Figure 4. Dq-Axis Voltages Under Proposed Hodo Based Pi With Novel Anti-Windup Scheme For Case 1. (A) Control Input On Q-Axis Vqs; (B) Control Input On D-Axis Vds.

Figure 5. Experimental Results Of The Proposed Hodo Based Pi With Novel Anti-Windup Scheme For Case 2. (A) Mechanical Speed Response Of Pmsm; (B) Mechanical Speed Error; (C) Estimated Load Torque Disturbance.

 

Figure 6. Dq-Axis Currents Of The Proposed Hodo Based Pi With Novel Anti-Windup Scheme For Case 2. (A) Ids And Its Desired Value Idsd; (B) Iqs And Its Desired Value Iqsd.

 

Figure 7. Dq-Axis Voltages Under The Proposed Hodo Based Pi With Novel Anti-Windup Scheme For Case 2. (A) Control Input On Q-Axis Vqs; (B) Control Input On D-Axis Vds.

 

Figure 8. Experimental Results Of The Baseline Control For Case 1. (A) Mechanical Speed Response Of Pmsm; (B) Mechanical Speed Error.

Figure 9. Dq-Axis Currents Of Baseline Control For Case 1. (A) Ids And Its Desired Value Idsd; (B) Iqs And Its Desired Value Iqsd.

Figure 10. Dq-Axis Voltages Of The Baseline Control For Case 1. (A) Control Input On Q-Axis Vqs; (B) Control Input On D-Axis Vds.

 

Figure 11. Experimental Results Of The Baseline Control For Case 2. (A) Mechanical Speed Response Of Pmsm; (B) Mechanical Speed Error.

CONCLUSION:

In this paper, disturbance observer based control for the PMSM prototyping kit is proposed. The cascade structure of discrete-time PI-PI control system equipped with tracking anti-windup scheme has been utilized for both loops. As the total disturbance estimation with HODO is based on the accurate prediction of the mechanical speed, the detailed motion equation of the PMSM has been derived. The motion equation in the proposed HODO includes terms associated with torque losses due to drag resulting from time-varying flux, friction, and hysteresis. It has demonstrated its ability to improve the speed tracking performance under the external disturbance and unmodelled dynamics associated with a cogging torque and a high-frequency electromagnetic noise in the PMSM system. The estimated total disturbance is compensated in the speed controller. A zero steady-state errors have been achieved in the real time experiment. The mechanical speed errors were minimized in both operation scenarios. The performances of the proposed and baseline control algorithms have been evaluated under mechanical speed and load torque variations. The performance of the novel control system has shown better robustness to the external disturbances.

REFERENCES:

[1] T. D. Do, H. H. Choi, and J.-W. Jung, ``Nonlinear optimal DTC design and stability analysis for interior permanent magnet synchronous motor drives,'' IEEE/ASME Trans. Mechatronics, vol. 20, no. 6, pp. 2716_2725, Dec. 2015.

[2] T. D. Do, Y. N. Do, and P. D. Dai, ``A robust suboptimal control system design of chaotic PMSMs,'' Electr. Eng., vol. 100, no. 3, pp. 1455_1466, Sep. 2018.

[3] B. Sarsembayev, K. Suleimenov, B. Mirzagalikova, and T. D. Do, ``SDRE- based integral sliding mode control for wind energy conversion systems,'' IEEE Access, vol. 8, pp. 51100_51113, 2020.

[4] T. D. Do, ``Optimal control design for chaos suppression of PM synchronous motors,'' in Proc. 2nd Int. Conf. Control Sci. Syst. Eng. (ICCSSE), Jul. 2016, pp. 88_92.

[5] J.-W. Jung, V. Q. Leu, T. D. Do, E.-K. Kim, and H. H. Choi, ``Adaptive PID speed control design for permanent magnet synchronous motor drives,'' IEEE Trans. Power Electron., vol. 30, no. 2, pp. 900_908, Feb. 2015.

Harmonic Voltage Control in Distributed Generation Systems Using Optimal Switching Vector Strategy

ABSTRACT:

 With increased penetration of renewable power and the nonlinear loads in the distributed generation (DG) systems, increased power quality concerns are exhibited in the active distribution networks, especially the challenges associated with the current and voltage harmonics in the system. Various conventional harmonic compensation techniques are developed for voltage-controlled DG inverters in past, majority involve either multiple proportional-integral (PI) or proportional-resonant (PR) controllers in eliminating grid current harmonics. The current controlled inverters, on the other hand, are not preferred in industrial applications, accounting to their wide variations in the switching frequency. A novel and adaptive harmonic voltage control is developed here, for voltage-controlled DG inverters, which neither uses any PI regulators nor imposes stability issues associated with nonideal implementation of infinite gains of PR controllers. Interestingly, the developed control logic can be used for DG inverters, both in grid-connected and off-grid operational modes. Furthermore, this strategy allows a network operator to use this as an additional supplement that can be enabled/disabled as per the network requirement. The control logic exploits the property of an optimal-switching-vector controller, i.e., accurate output voltage tracking. Simulations results demonstrate the effectiveness of the controller, to suppress grid current harmonics and load voltage harmonics in grid-interfaced (GI) and off-grid modes, respectively, ultimately satisfying the mandatory IEEE standard-1547. Experimental results verify the viability of the controller for practical applications.

KEYWORDS:

1.      Distributed generation (DG)

2.       Harmonics

3.      Optimal switching- vector (OSV) control and voltage source inverter (VSI)

      Power quality

SOFTWARE: MATLAB/SIMULINK

SCHEMATIC DIAGRAM:

Fig. 1. System configuration.

EXPECTED SIMULATION RESULTS:

Fig. 2. Salient internal signals of the harmonic voltage controller upon enabling the harmonic control switch (a) vpabc5, vpabc7, vpabc11, and vpabc13, (b) |vp|abc5, |vp|abc7, |vp|abc11, and |vp|abc13, (c) λpabc5, λpabc7, λpabc11, and λpabc13, and (d) vc abc5, vc abc7, vc abc11, and vc abc13.

Fig. 3. Reference voltages generated by the harmonic voltage controller.

Fig. 4. Salient internal signals of the OSV controller upon enabling the harmonic control switch (a) voαβ, ioαβ, and  vcαβ with SS1, and voαβ of future sampling instant with SS1, (b) “eα” of future sampling instant with SS1, MGPC with SS1, SS2, and SS3, and (c) MGPC with SS4, SS5, SS6, and SS0.

 

 

Fig. 5. Optimal minimization function and the corresponding switching sequences generated by the OSV controller.

 

Fig. 6. Performance of a single DG-VSI system in GI mode (a) without any harmonic voltage control and (b) with the presented control.

CONCLUSION:

A harmonic voltage control strategy using optimal switching vector controller has been explored for a three-phase grid connected and off-grid DG system. A minimization criterion is used in an OSV controller to achieve accurate output voltage tracking performance and flexibly control the DG output harmonic voltage. In this way, the harmonic currents entering the grid are precisely regulated in the grid-connected mode of operation. In stand-alone mode of operation, the power quality is improved by elimination of PCC voltage harmonics caused by nonlinear load in the system. The controller eliminates the usage of multiple PR controllers, PI regulators, cascaded feedback loops, or phase locked loops in the system. The simulation and Fig. 17. System performance with OSV-based harmonic control (a) vgab with iga and iLa, (b) salient internal signals of the OSV controller reference voltages corresponding to gating pulses, (c) VDC, iga, and harmonic currents absorbed by the DG, and (d) performance without any harmonic control—iLa, vgab, iga, and ioa. Fig. 18. (a) THD of vgab. (b) THD of iLa. (c) THD of iga. experimental performances are evaluated to confirm the viability of the algorithm. The employed modern DG systems increased renewables and are subject to rapidly increasing nonlinear loads, and the presented control strategy is a possible solution for voltage-controlled DG inverters. As this controller is possible to be appended in existing DG inverter controls, it can be easily enabled or disabled flexibly, as per the system operator need.

REFERENCES:

[1] D. E. Olivares et al., “Trends in microgrid control,” IEEE Trans. Smart Grid, vol. 5, no. 4, pp. 1905–1919, Jul. 2014.

[2] H. R. Baghaee, M. Mirsalim, G. B. Gharehpetian, and H. A. Talebi, “Decentralized sliding mode control of WG/PV/FC microgrids under unbalanced and nonlinear load conditions for on- and off-grid modes,” IEEE Syst. J., vol. 12, no. 4, pp. 3108–3119, Dec. 2018.

[3] IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources With Associated Electric Power Systems Interfaces, IEEE Standard 1547-2018, 2018.

[4] H. R. Baghaee, M. Mirsalim, G. B. Gharehpetan, and H. A. Talebi, “Nonlinear load sharing and voltage compensation of microgrids based on harmonic power-flow calculations using radial basis function neural networks,” IEEE Syst. J., vol. 12, no. 3, pp. 2749–2759, Sep. 2018.

[5] S. Priyank, and B. Singh, “Leakage current suppression in double stage SECS enabling harmonics suppression capabilities,” IEEE Trans. Energy Conv., vol. 36, no. 1, pp. 186–196, Mar. 2021.