Multifunctional Control of Wind-Turbine Based Nano-Grid Connected to a Distorted Utility-Grid

ABSTRACT:

 This paper proposes a multifunctional control strategy and associated control algorithms for distributed wind-turbine (WT) based nano-grids connected to a distorted utility-grid. The contribution is on a new strategy with innovative control algorithms to coordinate multiple converters for a multitasking operation of the nano-grids. The novelty is on a unique control design with feasibilities:maximizing the generated power from WT, maintaining power quality in both ac- and dc-sides under critical conditions of the power grid, and improving power quality against distortion from local nonlinear loads under a reduced switching frequency. A robust fast-dynamic predictive control method is developed for current controllers to fulfil the multifunction. Unconstrained deadbeat control inputs are derived in twofold targets: ensuring fast dynamic response and significantly reducing both the computation and switching frequency for finite predictive control. The control system is applied on a permanent-magnet synchronous generator (PMSG) WT-based nano-grid connected to a distorted utility-grid. An OPAL-RT-based real-time platform is used for comparative studies among the proportional integration (PI) control, finite predictive control (FS-MPC), and proposed control method. The performance verification exhibits the power quality improvement in both the nano- and utility-grids under critical conditions via high-performed regulation of currents, voltages, reactive power, and rotor speed of the PMSG-WT.

KEYWORDS:

1.      Deadbeat control

2.      Distortion

3.      Finite predictive control

4.      Harmonic

5.      Permanent magnet synchronous generator (PMSG)

6.      Wind energy conversion system

7.      Unbalanced and distorted grid

 

SOFTWARE: MATLAB/SIMULINK

SCHEMATIC DIAGRAM:

Fig. 1. A generic diagram of a WT-based nano-grid connected to a distribution grid.

 EXPECTED SIMULATION RESULTS:

 

 

Fig. 2. Rotor-speed dynamic tracking-performances of the WT for maximum power extraction under wind-speed turbulence (7%). (a) The conventional PI control (PI.), (b) The proposed multifunctional control with fast-dynamic response design (Pro.).

 

Fig. 3. Comparative speed and current regulation of the MSC control between the conventional FCS-MPC (Fcs.) – Left and proposed control method (Pro.) – Right, (a) Comparative dynamic performances under step-change of reference speed and current, (b) The current regulation and average switching frequency.

Fig. 4. Comparative switching behaviors in the MSC control, (a) The conventional FCS-MPC (Fcs.), (b) The proposed control method (Pro.).

Fig. 5. Comparative performances of the grid-injected current regulation in the grid-interface converter under critical disturbances from two-phase-to-ground fault at a medium voltage bus, (a) The PI control, (b) The Pro. control.

Fig. 6. Comparative performances from Matlab/Simulink on the grid-injected current regulation under critical disturbances in the grid-voltages (i.e., harmonics and unbalance), (a) The PI control, (b) The Pro. control.

Fig. 7. Verification results obtained from OPAL-RT-based real-time systems for the current regulation of Pro. under critical utility-grid conditions. (a) Two- phases-to-ground grid-fault (a and b), (b) Unbalanced and harmonic distortion in the utility-grid voltage.

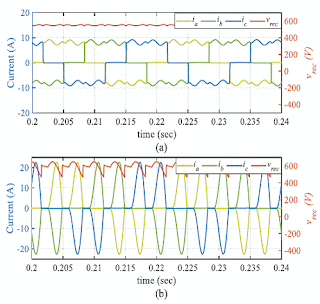
Fig. 8. Power quality compensation of the multifunction control in the nano-grid for distorted local loads. (a) Unbalanced and harmonic compensation for the local load currents, (b) Improvement of grid-voltages and grid-injected currents in a long-feeder connected to the nano-grid, reactive power compensation for the local loads.

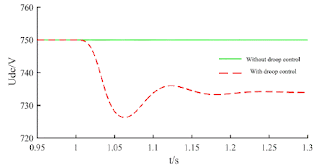
 CONCLUSION:

In this paper, a new multifunctional control strategy for WT-based nano-grids was proposed with an innovative direct control method for fast-dynamic response and reduced switching frequency. The approach in a context of a nano-grid enables multitasking operation by coordinating multiple converters in the nano-grid and efficiently utilizes the full-scaled capacity of the PMSG system. The new algorithm combines the fastest digital control (i.e., deadbeat laws) and finite set control to neglect the conventional exhaustive search, complicated prediction, and objective function evaluation while significantly reducing the average switching frequency. Fast-dynamic control components are embedded into conventional local controllers for multitasking operation. The coordination among converters in the nano-grid improves the performance of the WT-based nano-grid on optimal power tracking, voltage and current regulation, dc-voltage regulations, and power quality compensation in the utility-grid. This paper proves the benefits of a new approach by coordinating multiple converters in a broader context of nano-grids in multitasking operation where the rated power of converters can be efficiently exploited in comparison with the conventional grid-connected WT-systems. Comparative results demonstrate the efficacy of the proposed strategy and its potential to extensively apply to various applications in power electronics and power systems.

REFERENCES:

[1] V. Yaramasu and B. Wu, Model Predictive Control of Wind Energy Conversion Systems. IEEE Press, 2016.

[2] F. Blaabjerg and Z. Chen, POWER ELECTRONICS FOR MODERN WIND, vol. 1, no. 1. 2005.

[3] H. The N., A. S. Al-Sumaiti, V. P. Vu, A. Al-Durra, and T. D. Do, “Optimal power tracking of PMSG based wind energy conversion systems by constrained direct control with fast convergence rates,” Int. J. Electr. Power Energy Syst., 2020.

[4] A. Uehara et al., “A coordinated control method to smooth wind power fluctuations of a PMSG-Based WECS,” IEEE Trans. Energy Convers., 2011.

[5] V. Yaramasu, A. Dekka, M. J. Durán, S. Kouro, and B. Wu, “PMSG-based wind energy conversion systems: Survey on power converters and controls,” IET Electr. Power Appl., vol. 11, no. 6, pp. 956–968, 2017.

Modeling and Coordinated Control Design for Brushless Doubly-Fed Induction Generator-Based Wind Turbine to Withstand Grid Voltage Unbalance

ABSTRACT:

 

Grid codes require wind turbines to have capability to withstand a certain grid voltage unbalance without tripping. However, existing controls for brushless doubly-fed induction generator (BDFIG) based wind turbine under grid unbalance have many problems such as difficulty in realizing decoupling control, involvement with flux or current estimations, and complex control structure. Moreover, the existing studies only focused on the control of machine side converter (MSC), but the coordinated control between MSC and grid side converter (GSC) and the control objectives of overall BDFIG wind turbine system have not yet been addressed so far. To overcome these problems and improve the control capability, this paper proposes a coordinated control strategy by considering MSC and GSC together. First, the enhanced control objectives for overall BDFIG wind turbine system are determined. Second, the simple single current closed-loop controllers without involving with any flux or current estimations are designed for MSC and

GSC, respectively. Meanwhile, in current loops, all the disturbances and cross-coupling terms on dq axes are derived and used for feedforward control so as to achieve decoupling control and improve system dynamic response. Further, a fast sequence decomposition approach is employed to enhance the control characteristics of the whole system. Finally, the effectiveness of proposed control is validated through case studies for a 2 MW BDFIG based wind generation system. The results demonstrate that the proposed control can effectively achieve the control objectives of overall wind turbine system under grid voltage unbalance and provide excellent dynamic and stable performance.

 KEYWORDS:

1.      Brushless doubly-fed induction generator (BDFIG)

2.      Voltage unbalance

3.      Decoupling control

       Wind turbine

      Sequence decomposition

SOFTWARE: MATLAB/SIMULINK

BLOCK DIAGRAM:

Fig.1. configuration of BDFIG-based wind turbine system

 EXPECTED SIMULATION RESULTS:

 

 

Figure 2. Sequence Decomposition Results Of Grid Voltage With Notch Filter And Fast Decomposition Algorithm. (A) Grid Voltage Vgabc (P.U.). (B) Positive Sequence Component In __ Reference Frame (P.U.) (C) Negative Sequence Component In  Reference Frame (P.U.). (D) Positive Sequence Component In (Dq)C Reference Frame (P.U.). (E) Negative Sequence Component In (Dq)􀀀 Reference Frame (P.U.). (A) Decomposition Method With Notch Filter. (B) Fast Sequence Decomposition Algorithm

 

Figure 3. Waveforms With Elimination Of Torque Oscillations And Three Selectable Control Objectives Under 10% Grid Voltage Unbalance (!R D 0:7 P.U., " D 10%). (A) Total Output Current (P.U.). (B) Gsc D- Axis And Pw Q- Axis Currents (P.U.). (C) Gsc Q- Axis And Pw D-Axis Currents (P.U.). (D) Gsc Dc Axis And Qc Axis Currents (P.U.). (E)Total Output Active Power (P.U.). (F) Pw And Gsc Active Power (P.U.). (G) Total Output Reactive Power (P.U.). (H) Pw And Gsc Reactive Power (P.U.). (I) Electromagnetic Torque (P.U.). (J) Dc Link Voltage (P.U.).

Figure 4. Waveforms With Two Control Modes Under " D 10% Grid Voltage Unbalance (!R D 1:2 P.U.). (A) Total Output Current (P.U.). (B) Pw Voltage (P.U.). (C) Gsc Current (P.U.). (D) Cw Current (P.U.). (E) Total Output Active Power (P.U.). (F) Pw And Gsc Active Power (P.U.). (G) Total Output Reactive Power (P.U.). (H) Pw And Gsc Reactive Power (P.U.). (I) Bdfig Electromagnetic Torque (P.U.). (J) Dc Link Voltage (P.U.). (A) Control Mode 1. (B) Control Mode 2.

 

Figure 5. Waveforms With Variation Of Rotating Speed Under " D 10% Grid Voltage Unbalance. (A) Total Output Current (P.U.). (B) Cw Current (P.U.). (C) Total Output Active Power (P.U.). (D) Pw And Gsc Active Power (P.U.) (E) Total Output Reactive Power (P.U.). (F) Pw And Gsc Reactive Power (P.U.). (G) Mechanical Torque And Electromagnetic Torque (P.U.). (H) Rotor Rotating Speed (P.U.). (I) Dc Link Voltage (P.U.).

 

CONCLUSION:

In this paper, the mathematical model of BDFIG based wind turbine system under grid voltage unbalance is derived in detail. Based on such model, a coordinated control strategy by considering MSC and GSC together is proposed. Compared to existing controls, proposed control for MSC is greatly simplified and more applicable and has much better parameter robustness due to adopting single current loop control structure without involving with PW flux, CW flux, and rotor current estimations. Meanwhile, in cur- rent loop, all the cross-coupling terms and disturbances are derived and used for feedforward control, thus decoupling controls for the d-axis and q-axis currents as well as the average PW active and reactive power can be achieved. On the other hand, GSC is used to realize coordinated control with MSC so as to achieve three selectable enhanced control objectives, i.e., eliminating unbalanced total output current, oscillations of the total output active or reactive power. Further, a fast sequence decomposition approach instead of notch filers and enhanced PLL for MSC and GSC are employed to improve the control characteristics of the whole system. The effectiveness of proposed control is verified by means of theoretical analysis and case studies. The results demonstrated that the proposed control can improve the capability of withstanding grid voltage unbalance significantly and provide excellent dynamic and stable performance.

REFERENCES:

 

[1] W. Xu, M. G. Hussien, Y. Liu, M. R. Islam, and S. M. Allam, ``Sensorless voltage control schemes for brushless doubly-fed induction generators in stand-alone and grid-connected applications,'' IEEE Trans. Energy Convers., vol. 35, no. 4, pp. 1781_1795, Dec. 2020.

[2] Z. Li, X. Wang, M. Kong, and X. Chen, ``Bidirectional harmonic current control of brushless doubly fed motor drive system based on a fractional unidirectional converter under a weak grid,'' IEEE Access, vol. 9, pp. 19926_19938, 2021.

[3] Y. Cheng, B. Yu, C. Kan, and X.Wang, ``Design and performance study of a brushless doubly fed generator based on differential modulation,'' IEEE Trans. Ind. Electron., vol. 67, no. 12, pp. 10024_10034, Dec. 2020.

[4] F. Zhang, S. Yu, Y. Wang, S. Jin, and M. G. Jovanovic, ``Design and performance comparisons of brushless doubly fed generators with different rotor structures,'' IEEE Trans. Ind. Electron., vol. 66, no. 1, pp. 631_640, Jan. 2019.

[5] I. A. Gowaid, A. S. Abdel-Khalik, A. M. Massoud, and S. Ahmed, ``Ride-through capability of grid-connected brushless cascade DFIG wind turbines in faulty grid conditions_A comparative study,'' IEEE Trans. Sustain. Energy, vol. 4, no. 4, pp. 1002_1015, Oct. 2013.

Inertia And Damping Analysis Of Grid-Tied Photovoltaic Power Generation System With Dc Voltage Droop Control

ABSTRACT:

Photovoltaic power generation relies on power electronics and therefore does not have natural inertia and damping characteristics. In order to make the capacitance of the medium time scale participate in the grid frequency response without adding additional equipment, this paper takes the grid-connected photovoltaic power generation system based on DC voltage droop control as the research object, and establishes the static synchronous generator (SSG) model of the system. The model is used to analyze the main parameters affecting the inertia, damping and synchronization characteristics of the system and their influence laws. The research results show that the energy storage effect of the capacitor on the medium time scale can also make the system exhibit certain inertia characteristics. From the point of view of control parameters, as the droop coefficient Dp decreases, the inertia characteristic exhibited by the system is stronger. The larger the DC voltage outer loop proportional coefficient Kp is, the stronger the damping effect of the system is. The larger the DC voltage outer loop integral coefficient Ki, the stronger the synchronization capability of the system. In addition, the MATLAB/Simulink simulation platform is used to verify the correctness of the theoretical analysis results.

KEYWORDS:

1.      Grid-connected photovoltaic power generation system

2.      DC voltage droop control

3.      Inertia characteristic

4.      Damping effect

5.      Synchronization ability

 

SOFTWARE: MATLAB/SIMULINK

SCHEMATIC DIAGRAM:

 Figure 1. Grid-Connected Photovoltaic Power Generation System Based On Dc Voltage Droop Control.

 EXPECTED SIMULATION RESULTS

Figure 2. Influence Of Different Parameter Changes On System Inertia.

Figure 3. Influence Of Different Parameter Changes On System Inertia.

Figure 4. Influence Of Droop Coefficient Dp On Dc Voltage.

Figure 5. Influence Of Droop Coefficient Dp On System Power.

Figure 6. The Influence Of P Controller On Dc Voltage.

Figure 7. The Influence Of P Controller On System Power.

Figure 8. The Influence Of I Controller On Dc Voltage.

Figure 9. The Influence Of I Controller On System Power.

 CONCLUSION:

 This paper introduces a new GFC scheme for PV systems that do not employ real-time estimation of the MPP and make optimal use of the limited power reserves. By operating in full or limited grid-forming mode, the PV plant preserves its voltage source nature and manages to assist the grid during disturbances similarly or even better than synchronous machines. The modified current saturation scheme performs smoothly, without any need for fault detection or control switching.  Replacing SMs with PV GFC results in improved frequency profile during load disturbances due to faster response from the PV plant, and comparable terminal voltage profiles during faults despite the strict inverter over current limits. However, the PV GFC introduces another source of disturbances to the power system resulting from irradiance transients during cloud movement.

Inverters in GFL mode with ancillary services can support the grid during disturbances, but the contribution becomes limited as the system strength decreases. The GFC mode of inverter operation is the way forward for the renewables-rich and inverter-dominated power systems of the future.  Future work involves a complete investigation of the dynamic interactions between GFC and GFL inverters and the rest of the power system at various sizes and generation mixtures. Similarly, a methodology to determine the appropriate ratio of GFC and GFL resources would be very useful in converter-dominated power systems. Furthermore, the proposed method is designed for uniform illumination, which is the common assumption for utility-scale PV systems; an extension of the method to partial shading would improve its credibility and reliability at all possible conditions.

REFERENCES:

[1] F. Milano, F. Dörfler, G. Hug, D. J. Hill, and G. Verbič, "Foundations and challenges of low-inertia systems (Invited Paper)," Power Syst. Comp. Conf. (PSCC), Dublin, Ireland, 2018.

[2] C. Loutan, P. Klauer, S. Chowdhury, S. Hall, M. Morjaria, V. Chadliev, N. Milam, C. Milan, and V. Gevorgian, “Demonstration of essential reliability services by a 300-MW solar photovoltaic power plant,” National Renewable Energy Lab. (NREL), Golden, CO, United States, Rep. NREL/TP-5D00-67799, 2017.

[3] ENTSO-E, “Need for synthetic inertia (SI) for frequency regulation: ENTSO-E guidance document for national implementation for network codes on grid connection,” ENTSO-E, Brussels, Belgium, Tech. Guideline, Jan. 2018.

[4] J. C. Hernandez, P. G. Bueno, and F. Sanchez-Sutil, “Enhanced utility-scale photovoltaic units with frequency support functions and dynamic grid support for transmission systems,” IET Ren. Power Gen., vol. 11, no. 3, pp. 361-372, Jan. 2017.

[5] C. Guo, S. Yang, W. Liu, C. Zhao, and J. Hu, "Small-signal stability enhancement approach for VSC-HVDC system under weak AC grid conditions based on single-input single-output transfer function model," IEEE Trans. Power Del., to be published. DOI: 10.1109/TPWRD.2020.3006485.

 

Impacts of Grid Voltage Harmonics Amplitude and Phase Angle Values on Power Converters in Distribution Networks

ABSTRACT:

Motor drive systems based on diode-rectifier are utilised in many industrial and commercial applications due to their cost-effectiveness and simple topology. However, these diode rectifier-based systems can be affected by power quality and harmonics in distribution networks. Thus, this paper investigates the impact of grid voltage harmonics on the operation of power converters with three-phase diode rectifier using mathematical formulation of the drive voltage and current harmonics based on grid voltage harmonics. Simulation analysis and practical tests have been then carried out to validate the mathematical equations and the impact of grid voltage harmonics on the power converter harmonics. The results illustrate that even a small amount of grid voltage harmonics (around 4%) could significantly impact the input current harmonic contents of the three-phase diode rectifier. It is also shown that the phase-angle of grid voltage harmonics plays a crucial role to improve or deteriorate the input current harmonics of the power converters. In the next step, the optimum condition of grid voltage harmonics to minimise the input current harmonics has been evaluated and verified based on different grid codes. Finally, a harmonic mitigation technique in multi-drive systems using Electronic Inductor is proposed to mitigate the current harmonics at the PCC.

KEYWORDS:

1.      Distorted grid

2.      Distribution networks

3.      Total harmonic distortion

4.      Three-phase rectifier

  Voltage harmonics

SOFTWARE: MATLAB/SIMULINK

CIRCUIT DIAGRAM:

Figure 1. Simulink Model For The Tested Asd Under The Presence Of Voltage Harmonics At The Pcc.

 EXPECTED SIMULATION RESULTS:

 

Figure 2. Simulation Results Of The Three-Phase Input Currents And Vrec

In Case: (A) 1, (B) 2, And (C) 3.

Figure 3. Practical Measurements Of The Three-Phase Input Currents And Vrec In Cases: (A) 1, (B) 2, And (C) 3.

 

Figure 4. Simulation Results Of The Three-Phase Input Currents And Vrec

In Cases: (A) Ieee-Min, (B) Ieee-Max.

Figure 5. Practical Measurements Of The Three-Phase Input Currents

And Vrec In Cases: (A) Ieee-Min, (B) Ieee-Max.

Figure 6. Simulation Results For Phase ``A'' Current When U1 Mitigates

Harmonics Generated By U2: (A) Case 3, (B) Ieee-Max Case.

 

Figure 7. Simulation Results For Output Voltage (Vo), Inductor Current, And Phase ``A'' Inverter Side Current Of U1.

CONCLUSION:

 

In this paper, the impact of grid voltage distortion on power converter current harmonics emission has been investigated. For that aim, ASDs with conventional diode rectifier has been considered to represent the power electronic system. A mathematical formulation of the rectified voltage, inductor current, and input currents of a three-phase diode rectifier is derived under the presence of voltage harmonics at the PCC. Different cases of voltage harmonics are then considered in the analysis to investigate the behaviour of the rectified voltage and the input current harmonics. The results show that the presence of even a small level of voltage harmonics (4%) at the PCC can change the current THDi by up to 30%. Furthermore, it has been shown that the phase-angle of the voltage harmonics can have a significant impact on the input current harmonics. Depending on the voltage harmonic phase-angle, the same amount of voltage harmonics could improve or deteriorate the rectified voltage ripple and the input current THDi. Moreover, the voltage harmonic phase-angle could create a phase delay (1) in the diodes conduction time. A positive 1 impacts the displacement power factor negatively, whereas a negative 1 improves that factor. Finally, a harmonic mitigation technique to compensate the high level of current harmonics using Electronic Inductor (EI) is presented.

REFERENCES:

[1] B. K. Bose, ``Power electronics and motor drives recent progress and perspective,'' IEEE Trans. Ind. Electron., vol. 56, no. 2, pp. 581_588, Feb. 2009.

[2] B. K. Bose, ``Energy, environment, and advances in power electronics,'' IEEE Trans. Power Electron., vol. 15, no. 4, pp. 688_701, Jul. 2000.

[3] W. Gray and F. Haydock, ``Industrial power quality considerations when installing adjustable speed drive systems,'' in Proc. IEEE Cement Ind. Tech. Conf. XXXVII Conf. Rec., San Juan, PR, USA, Jun. 1995, pp. 17_33.

[4] P. Waide and C. U. Brunner, ``Energy-ef_ciency policy opportunities for electric motor-driven systems,'' Int. Energy Agency, Paris, France, Work. Paper, 2011, pp. 1_128.

[5] B. Singh, B. N. Singh, A. Chandra, K. Al-Haddad, A. Pandey, and D. P. Kothari, ``A review of three-phase improved power quality AC-DC converters,'' IEEE Trans. Ind. Electron., vol. 51, no. 3, pp. 641_660, Jun. 2004.