Transformer less Inverter with Virtual DC Bus Concept for Cost-Effective Grid-Connected PV Power Systems

Transformer less Inverter with Virtual DC Bus Concept for Cost-Effective Grid-Connected PV Power Systems

ABSTRACT:

In order to eliminate the common-mode (CM) leakage current in the transformer less photovoltaic (PV) systems, the concept of the virtual dc bus is proposed in this paper. By connecting the grid neutral line directly to the negative pole of the dc bus, the stray capacitance between the PV panels and the ground is bypassed. As a result, the CM ground leakage current can be suppressed completely. Meanwhile, the virtual dc bus is created to provide the negative voltage level for the negative ac grid current generation. Consequently, the required dc bus voltage is still the same as that of the full-bridge inverter. Based on this concept, a novel transformer less inverter topology is derived, in which the virtual dc bus is realized with the switched capacitor technology. It consists of only five power switches, two capacitors, and a single filter inductor. Therefore, the power electronics cost can be curtailed. This advanced topology can be modulated with the uni polar sinusoidal pulse width modulation (SPWM) and the double frequency SPWM to reduce the output current ripple. As a result, a smaller filter inductor can be used to reduce the size and magnetic losses. The advantageous circuit performances of the proposed transformer less topology are analyzed in detail, with the results verified by a 500-W prototype.

KEYWORDS

1.      Common mode (CM) current

2.       Photovoltaic (PV) system

3.       Switched capacitor

4.       Transformer less inverter

5.       Unipolar sinusoidal pulse width modulation (SPWM)

6.       Virtual dc bus.

SOFTWARE: MATLAB/SIMULINK

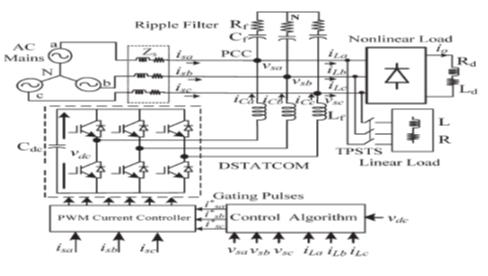
BLOCK DIAGRAM:

Fig.1. Proposed topology.

 EXPECTED SIMULATION RESULTS:

Fig.2. Output current and grid voltage.

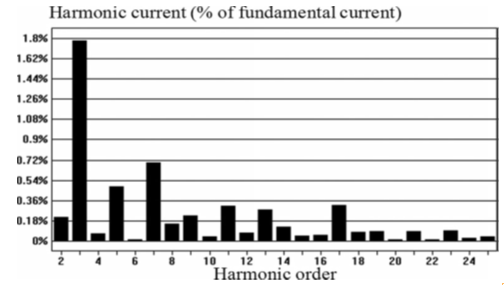
Fig.3. Current harmonics distribution.

                                             

Fig.4. Simulation waveform for reactive power generation

Fig.5. Current stress on S₃ .

Fig. 6. Enlarged figure for current stress on S₃

.                                     

 Fig. 7. CM current of H5 circuit.

Fig. 8. Current stress under different capacitor ratios for the proposed circuit: (a) C₁ /C₂ = 1/2; (b) C₁ /C₂ = 2/1.

             

CONCLUSION:

The concept of the virtual dc bus is proposed to solve the CM current problem for the transformer less grid-connected PV inverter. By connecting the negative pole of the dc bus directly to the grid neutral line, the voltage on the stray PV capacitor is clamped to zero. This eliminates the CM current completely. Meanwhile, a virtual dc bus is created to provide the negative voltage level. The required dc voltage is only half of the half bridge solution, while the performance in eliminating the CM current is better than the full-bridge-based inverters. Based on this idea, a novel inverter topology is proposed with the virtual dc bus concept by adopting the switched capacitor technology. It consists of only five power switches and a single filter inductor. The proposed topology is especially suitable for the small-power single-phase applications, where the output current is relatively small so that the extra current stress caused by the switched capacitor does not cause serious reliability problem for the power devices and capacitors. With excellent performance in eliminating the CM current, the virtual dc bus concept provides a promising solution for the transformer less grid-connected PV inverters.

REFERENCES:

[1] J. P. Benner and L. Kazmerski, “Photovoltaics gaining greater visibility,” IEEE Spectr., vol. 36, no. 9, pp. 34–42, Sep. 1999.

[2] Z. Zhao, M. Xu, Q. Chen, J.-S. Lai, and Y. Cho, “Derivation of boost-buck converter based high-efficiency robust PV inverter,” in Proc. IEEE Energy Convers. Cong. Expos., Sep. 12–16, 2010, pp. 1479–1484.

[3] R.W. Erickson and A. P. Rogers, “A microinverter for building-integrated photovoltaics,” in Proc. 24th Annu. IEEE Appl. Power Electron. Conf. Expos., Feb. 15–19, 2009, pp. 911–917.

[4] S. B. Kjaer, J. K. Pedersen, and F. Blaabjerg, “A review of single-phase grid-connected inverters for photovoltaic modules,” IEEE Trans. Ind. Appl., vol. 41, no. 5, pp. 1292–1306, Sep./Oct. 2005.

[5] E. Koutroulis and F. Blaabjerg, “Design optimization of grid-connected PV inverters,” in Proc. 26th Annu. IEEE Appl. Power Electron. Conf. Expos., Mar. 6–11, 2011, pp. 691–698.

Dynamic Simulation of a Three-Phase Induction Motor Using Matlab Simulink

Dynamic Simulation of a Three-Phase Induction Motor Using Matlab Simulink

ABSTRACT:

 The theory of reference frames has been effectively used as an efficient approach to analyze the performance of the induction electrical machines. This paper presents a step by step Simulink implementation of an induction machine using dq0 axis transformations of the stator and rotor variables in the arbitrary reference frame. For this purpose, the relevant equations are stated at the beginning, and then a generalized model of a three-phase induction motor is developed and implemented in an easy to follow way. The obtained simulated results provide clear evidence that the reference frame theory is indeed an attractive algorithm to demonstrate the steady-state behavior of the induction machines.

 SOFTWARE: MATLAB/SIMULINK

 BLOCK DIAGRAM:

Figure 1 the 3-phase induction motor Matlab/Simulink model

EXPECTED SIMULATION RESULTS:

Figure 2 Torque speed characteristics for the 3 hp induction motor

Figure 3 Machine variables during free acceleration of a 3-hp induction motor

Figure 4 Torque speed characteristics for the 2250 hp induction motor

Figure  5 Machine variables during free acceleration  of a 2250-hp induction motor  

            

CONCLUSION:

In this paper, an implementation and dynamic modeling of a three-phase induction motor using Matlab/Simulink are presented in a step-by-step manner. The model was tested by two different ratings of a small and large induction motors. The two simulated machines have given a satisfactory response in terms of the torque and speed characteristics. Also, the model was evaluated by Matlab m-file coding program. Both methods have given the same results for the same specifications of the three phase induction motors used in this simulation. This concludes that the Matlab/Simulink is a reliable and sophisticated way to analyze and predict the behavior of induction motors using the theory of reference frames.

REFERENCES:

[1] P. C. Krause, O. Wasynczuk, S. D. Sudhoff “Analysis of Electric Machinery and Drive Systems”, IEEE Press, A John Wiley & Sons, Inc. Publication Second Edition, 2002.

[2] P.C. Krause and C. H. Thomas, “Simulation of Symmetrical Induction Machinery”, IEEE Transaction on Power Apparatus and Systems, Vol. 84, November 1965, pp. 1038-1053.

[3] P. C. Krause, “Analysis of Electric Machinery”, McGraw-Hill Book Company, 1986.

[3] D. C. White and H. H. Woodson, “Electromechanical Energy Conversion”, John Wiley and Sons, New York, 1959.

[4] M. L. de Aguiar, M. M. Cad, “The concept of complex transfer functions applied to the modeling of induction motors”, Power Engineering Society Winter Meeting, 2000, pp. 387–391.

[5] S. Wade, M. W. Dunnigan, B. W. Williams, “Modeling and simulation of induction machine vector control with rotor resistance identification”, IEEE Transactions on Power Electronics, vol. 12, No. 3, May 1997, pp. 495–506.

Implementation of Adaptive Filter in Distribution Static Compensator

Implementation of Adaptive Filter in Distribution Static Compensator

ABSTRACT:

This paper presents an implementation of an adaptive filter in a three-phase distribution static compensator (DSTATCOM) used for compensation of linear/nonlinear loads in a three-phase distorted voltage ac mains. The proposed filter, which is based on adaptive synchronous extraction, is used for extraction of fundamental active- and reactive-power components of load currents in estimating the reference supply currents. This control algorithm is implemented on a developed DSTATCOM for reactive-power compensation, harmonics elimination, load balancing, and voltage regulation under linear and nonlinear loads. The performance of DSTATCOM is observed satisfactory under unbalanced time-varying loads.

KEYWORDS

1.      Adaptive filter (AF)

2.      distribution static compensator (DSTATCOM)

3.       harmonics

4.       load balancing

5.       sinusoidal tracking algorithm

6.       voltage-source converter (VSC)

SOFTWARE: MATLAB/SIMULINK

 BLOCK DIAGRAM:

Fig.1. Schematic of three-leg DSTATCOM.

EXPECTED SIMULATION RESULTS:

                                                            (a)

                                                              (b)

Fig. 2. (a), (b), and (c) Various intermediate signals of the control algorithm at load injection. (a) Ch. 1 and 2: 200 V/div; Ch. 3 and 4: 20 A/div; Time axis: 50 ms/div. (b) Ch. 1, 2, 3, and 4: 20 A/div; Time axis: 20 ms/div. (c) Ch. 1, 2,3, and 4: 20 A/div; Time axis: 20 ms/div.

 Fig. 3. Steady-state performance of DSTATCOM at linear lagging PF load in PFC mode. (a) P_s. (b) P_L. (c) P_c. (d) v_ab, i_sa. (e) v_bc, i_sb. (f) v_ca, i_sc.

 Fig. 4. Steady-state performance of DSTATCOM at nonlinear loads in PFC mode. (a) v_ab, i_sa. (b) v_bc, i_sb. (c) v_ca, i_sc. (d) Harmonic spectrum of i_sa. (e) v_ab, i_La. (f) Harmonic spectrum of i_La.   

Fig. 5. Dynamic performance of DSTATCOM at unbalanced linear loads. (a) v_ab, i_sa, i_sb, i_sc. (b) v_ab, i_La, i_Lb, i_Lc. (c) v_dc, i_sa, i_Ca, i_La.

Fig. 6. Dynamic performance of DSTATCOM at unbalanced nonlinear loads. (a) v_ab, i_sa, i_sb, i_sc. (b) v_ab, i_La, i_Lb, i_Lc. (c) v_dc, i_sa, i_Ca, i_La

.

Fig. 7. Steady-state performance of DSTATCOM at linear lagging PF load in ZVR mode. (a) P_s. (b) P_L. (c) P_c. (d) v_ab, i_sa. (e) v_bc, i_sb. (f) v_ca, i_sc.

Fig. 8. Steady-state performance of DSTATCOM at nonlinear load in ZVR mode. (a) v_ab, i_sa. (b) v_bc, i_sb. (c) v_ca, i_sc. (d) Harmonic spectrum of i_sa. (e) Harmonic spectrum of i_La. (f) i_Ca. (g) P_s. (h) P_L.

 

Fig. 9. Variation of V_t, i_sa, and i_La with v_dc under unbalanced linear loads.

CONCLUSION:

A DSTATCOM has been implemented for a three-phase distribution system. An AF has been used for control of DSTATCOM. This AF has been found simple and easy to implement, and its performance has been observed satisfactory with nonsinusoidal and distorted voltages of ac mains under load variation. The performance of DSTATCOM with its AF has been demonstrated for harmonics elimination, reactivepower compensation, and load balancing with self-supporting dc link in PFC and ZVR modes. The dc-link voltage of the DSTATCOM has been also regulated to a desired value under time-varying load conditions.

REFERENCES:

[1] E. F. Fuchs and M. A. S. Mausoum, Power Quality in Power Systems and Electrical Machines. London, U.K.: Elsevier, 2008.

[2] H. Akagi, E. H. Watanabe, and M. Aredes, Instantaneous Power Theory and Applications to Power Conditioning. Hoboken, NJ, USA: Wiley, 2007.

[3] A. Emadi, A. Nasiri, and S. B. Bekiarov, Uninterruptible Power Supplies and Active Filters. Boca Raton, FL, USA: CRC Press, 2005.

[4] J. Jacobs, D. Detjen, C. U. Karipidis, and R. W. De Doncker, “Rapid prototyping tools for power electronic systems: Demonstration with shunt active power filters,” IEEE Trans. Power Electron., vol. 19, no. 2, pp. 500– 507, Mar. 2004.

[5] A. Ghosh and G. Ledwich, Power Quality Enhancement Using Custom Power Devices. New Delhi, India: Springer Int. Edition, 2009.

Improved Active Power Filter Performance for Renewable Power Generation Systems

Improved Active Power Filter Performance for Renewable Power Generation Systems

ABSTRACT

An active power filter implemented with a four-leg voltage-source inverter using a predictive control scheme is presented. The use of a four-leg voltage-source inverter allows the compensation of current harmonic components, as well as unbalanced current generated by single-phase nonlinear loads. A detailed yet simple mathematical model of the active power filter, including the effect of the equivalent power system impedance, is derived and used to design the predictive control algorithm. The compensation performance of the proposed active power filter and the associated control scheme under steady state and transient operating condition is demonstrated through simulations and experimental results.

KEYWORDS

1.      Active power filter

2.      Current control four-leg converters,

3.      Predictive control.

SOFTWARE: MATLAB/SIMULINK

BLOCK DIAGRAM:

Fig. 1. Three-phase equivalent circuit of the proposed shunt active power filter.

CONTROL BLOCK DIAGRAM:

Fig.2. dq-based current reference generator block diagram.

                        

EXPECTED SIMULATION RESULTS:

Fig. 3. Simulated waveforms of the proposed control scheme. (a) Phase to neutral source voltage. (b) Load Current. (c) Active power filter output current. (d) Load neutral current. (e) System neutral current. (f) System currents. (g) DC voltage converter.

Fig. 4. Experimental transient response after APF connection. (a) Load Current iLu , active power filter current iou , dc-voltage converter vdc , and system current isu . Associated frequency spectrum. (c) Voltage and system waveforms, vsu and isu , isv , isw . (d) Current reference signals i∗ ou , and active power filter current iou (tracking characteristic).

Fig. 5. Experimental results for step load change (0.6 to 1.0 p.u.). Load Current iLu , active power filter current iou , system current isu , and dc-voltage converter vdc .

Fig. 6. Experimental results for step unbalanced phase u load change (1.0 to 1.3 p.u.). (a) Load Current iLu , load neutral current iLn , active power filter neutral current ion , and system neutral current isn . (b) System currents isu , isv , isw , and isn .

CONCLUSION:

Improved dynamic current harmonics and a reactive power compensation scheme for power distribution systems with generation from renewable sources has been proposed to improve the current quality of the distribution system. Advantages of the proposed scheme are related to its simplicity, modeling, and implementation. The use of a predictive control algorithm for the converter current loop proved to be an effective solution for active power filter applications, improving current tracking capability, and transient response. Simulated and experimental results have proved that the proposed predictive control algorithm is a good alternative to classical linear control methods. The predictive current control algorithm is a stable and robust solution. Simulated and experimental results have shown thecompensation effectiveness of the proposed active power filter.

REFERENCES:

[1] J. Rocabert, A. Luna, F. Blaabjerg, and P. Rodriguez, “Control of power converters in AC microgrids,” IEEE Trans. Power Electron., vol. 27, no. 11, pp. 4734–4749, Nov. 2012.

[2] M. Aredes, J. Hafner, and K. Heumann, “Three-phase four-wire shunt active filter control strategies,” IEEE Trans. Power Electron., vol. 12, no. 2, pp. 311–318, Mar. 1997.

[3] S. Naidu and D. Fernandes, “Dynamic voltage restorer based on a four leg voltage source converter,” Gener. Transm. Distrib., IET, vol. 3, no. 5, pp. 437–447, May 2009.

[4] N. Prabhakar and M. Mishra, “Dynamic hysteresis current control to minimize switching for three-phase four-leg VSI topology to compensate nonlinear load,” IEEE Trans. Power Electron., vol. 25, no. 8, pp. 1935–1942, Aug. 2010.