ABSTRACT:
The Proportional Resonant (PR) current
controller provides gains at a certain frequency (resonant frequency) and
eliminates steady state errors. Therefore, the PR controller can be
successfully applied to single grid-connected PV inverter current control. On
the contrary, a PI controller has steady-state errors and limited disturbance
rejection capability. Compared with the L- and LC filters, the LCL filter has
excellent harmonic suppression capability, but the inherent resonant peak of
the LCL filter may introduce instability in the whole system. Therefore,
damping must be introduced to improve the control of the system. Considering
the controller and the LCL filter active damping as a whole system makes the
controller design method more complex. In fact, their frequency responses may
affect each other. The traditional trial-and-error procedure is too
time-consuming and the design process is inefficient. This paper provides a
detailed analysis of the frequency response influence between the PR controller
and the LCL filter regarded as a whole system. In addition, the paper presents
a systematic method for designing controller parameters and the capacitor
current feedback coefficient factor of LCL filter active-damping. The new
method relies on meeting the stable margins of the system. Moreover, the paper
also clarifies the impact of the grid on the inverter output current. Numerical
simulation and a 3 kW laboratory setup assessed the feasibility and
effectiveness of the proposed method.
KEYWORDS:
1. Single
phase
2. Grid-connected
3. LCL
filter
4. Active
damping
5. Proportional
resonant (PR) controller
SOFTWARE: MATLAB/SIMULINK
CIRCUIT DIAGRAM:
Figure 1. Two-stage
single-phase PV system with LCL-filter control scheme.
EXPECTED SIMULATION RESULTS:
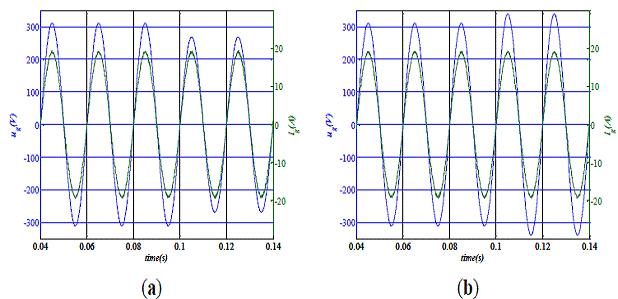
Figure 3. Grid voltage and injected current at
full load with inductor L1 variation: simulation results. (a) Inductor L1 increased by
20%: grid voltage sag; (b)
Inductor L1 increased by 20%: grid voltage swell; (c) Inductor L1 decreased by
20%: grid voltage sag; (b)
Inductor L1 decreased by 20%: grid voltage swell.
Figure 4. Grid voltage and injected current at
full load with inductor L2 variation: simulation results. (a) Inductor L2 increased by
150%: grid voltage sag; (b)
inductor L2 increased by 150%: grid voltage swell; (c) inductor L2 decreased by
20%: grid voltage sag; (b)
inductor L2 decreased by 20%: grid voltage swell.
Figure 5. Grid voltage and injected current at
full load with capacitor C variation: simulation results. (a) Capacitor C increased by
20%: grid voltage sag; (b)
capacitor C increased by 20%: grid voltage swell; (c) capacitor C decreased by
20%: grid voltage sag; (b)
capacitor C decreased by 20%: grid voltage swell.
The
stability analysis of the system composed by a PR controller and an LCL filter
together is not easy: the frequency responses may affect each other and the PR
controller design becomes complex. The traditional method based on
trial-and-error procedures, is too time-consuming, and the design process is
inefficient. This paper provides a detailed analysis of the frequency response
influence between the PR controller and the LCL filter. In addition, the paper
presents a systematic design method for the PR controller parameters and the
capacitor current feedback coefficient, used in the active damping of the LCL
filter. Using the new parameters, a numerical simulation shows that the system
meets the requirements of stable margins and current tracking steady-state
error. The robustness of the current controller is verified through several
experimental tests carried out on a 3 kW platform varying the system
parameters. The Bode diagrams of the system varying inductor, capacitor, and
grid impedance values confirmed that the controller parameters enhance
robustness against the system parameters variation. Moreover, the system
remains stable even in case of grid voltage fluctuation. Both the simulation
and the experimental results assess the validity of the proposed design method.
REFERENCES:
1. Carrasco, J.M.;
Franquelo, L.G.; Bialasiewicz, J.T.; Galvan, E.; Guisado, R.C.P.; Prats, A.M.;
Leon, J.I.; Moreno-Alfonso, N. Power-electronic systems for the grid
integration of renewable energy sources: A survey. IEEE Trans. Ind.
Electron. 2006, 53, 1002–1016.
2. Wessels, C.;
Dannehl, J.; Fuchs, F.W. Active Damping of LCL-Filter Resonance based on
Virtual Resistor for PWM Rectifiers—Stability Analysis with Different Filter
Parameters. In Proceedings of the 2008 IEEE Power Electronics Specialists
Conference, Rhodes, Greece, 15–19 June 2008; pp. 3532–3538.
3. Castilla, M.;
Miret, J.; Matas, J.; de Vicuna, L.G.; Guerrero, J.M. Control design guidelines
for single-phase grid-connected photovoltaic inverters with damped resonant
harmonic compensators. IEEE Trans. Ind. Electron. 2009, 56,
4492–4501.
4. Yi, L.;
Zhengming, Z.; Fanbo, H.; Sizhao, L.; Lu, Y. An Improved Virtual Resistance
Damping Method for Grid-Connected Inverters with LCL Filters. In Proceedings of
the 2011 IEEE Energy Conversion Congress and Exposition (ECCE 2011), Phoenix,
AZ, USA, 17–22 September 2011; pp. 3816–3822.
5.
Parker, S.G.; McGrath, B.P.; Holmes, D.G. Regions of Active Damping Control for
LCL Filters. In Proceedings of the Energy Conversion Congress and Exposition
(ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 53–60.