Performance Enhancement of Shunt Active Power filter using a Kalman Filter based H∞ Control Strategy

ABSTRACT

This paper proposes a Kalman filter (KF) based H∞ control scheme for a three phase shunt active power filter (SAPF) system. For the current control loop, a H∞ controller is designed with a mixed sensitivity approach for achieving stability and high disturbance rejection in the SAPF system. A new current reference scheme is also proposed that employs KF to avoid synchronization circuit and proportional integral (PI) controller loop resulting in a reliable and cost-effective SAPF system. This reference scheme can self-regulate the dc-link voltage by a fast and adaptive estimation of the source reference current with power system perturbations raised in source or load sides. The efficacy of the proposed KF-H∞ control algorithm is evaluated through comparison with an existing PI and PI plus vector PI (PI-PIVPI) algorithm and then validated with experimental studies pursued using a dSPACE1104. From the obtained experimental results, it is observed that the proposed SAPF significantly outperforms the existing PI-PIVPI in terms of exhibiting robustness to modeling uncertainties and insensitivity to grid perturbations such as harmonics, measurement noise and phase angle jump. Thus, the power quality improvement is achieved in terms of perfect current harmonics cancellation as well as power factor improvement.

KEYWORDS:

1.      Active power filter

2.      Self-regulate

3.      Robustness

4.      Power quality

5.      Harmonics cancellation

6.      Power factor improvement

SOFTWARE: MATLAB/SIMULINK

CIRCUIT DIAGRAM:

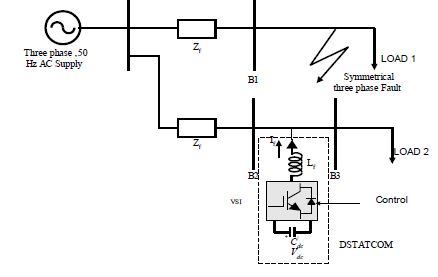
Fig.1 Proposed SAPF Control Scheme

EXPECTED SIMULATION RESULTS:

Fig.2 Test Case-1:(a) three-phase supply voltages, (b) three-phase load currents

Fig.3 Test Case-1:(a) three-phase source reference currents in proposed

method, (b) three-phase compensating currents in proposed method, (c) dclink

voltage in proposed method

Fig.4. Test Case-1: Harmonic spectra of (a) phase-a load current, (b) phase a

source current in the Proposed method, and (c) phase-a source current in the

Existing method

Fig.5.Test Case-2: Waveforms of three phase source currents, (i) Proposed

Method, (ii) Existing Method

Fig. 6. Test Case-2: Harmonic spectra of (a) phase-a source current in

Proposed Method, and (b) phase-a source current in Existing Method

Fig.7.Test Case -3: (a) three phase load currents, (b) dc-link voltage in

proposed method

Fig. 8 Test Case -3: (a) Waveforms of three phase compensating currents,

(b) Waveforms of three phase source currents , (i) Proposed Method, (ii)

Existing Method

Fig. 9 Test Case-3: Harmonic spectra of (a) phase-a load current, (b)

phase-a source current in Proposed Method, and (c) phase-a source current in

Existing Method

Fig. 10.Test Case-4: (a) Three phase supply voltages, (b) Three phase load

currents, (c) Three phase compensating currents in Proposed Method

Fig. 11. Case-4: Waveforms of three phase source currents and dc-link

voltage, (i) Proposed Method, (ii) Existing Method

Fig. 12. Test Case-4: Harmonics spectra of (a) phase-a load current, (b) phasea

source current in Proposed Method, and (c) phase-a source current in

Existing Method

Fig. 13. Test Case-5: Harmonics spectra of (a) phase-a load current, (b) phasea

source current in Proposed Method, and (c) phase-a source current in

Existing Method

CONCLUSION

In this paper, a H∞ controller with a new reference current estimation scheme based on KF has been proposed for a SAPF. This reference generation scheme is simple yet reliable and self regulator of dc-link voltage without having a PI controller. Only source current sensors are sufficient to determine the reference current, which decreases the effective cost of SAPF implementation. Further, H∞ current controller is designed with a proper selection of weighting functions to specify the robustness, control effort performance and error tracking performance of SAPF. Finally, the effectiveness of the proposed KF-H∞ control strategy was verified through various experimental tests, where the proposed control strategy presented good steady state as well as dynamic performance against supply or load variations. Generally power line uncertainties such as fluctuation of load, variation of system parameter, sudden failure of power system components and sensor nonlinearities degrade the reliability and efficiency of the SAPF system. Moreover, grid perturbations such as harmonics, measurement noise and phase angle jump are responsible for power quality deterioration. Hence, the objective of designing a robust control strategy in SAPF is achieved by accommodating all the possible perturbations occurring in the power system. From the experimental results, it is also observed that the proposed KF-H∞ control approach to design a SAPF is found to be robust in face parametric uncertainties due to grid perturbations yielding improvement in power quality more effectively in terms of tracking error reduction and efficient current harmonics mitigation.

REFERENCES

[1] O. Dordevic, M. Jones and E. Levi, ―Analytical formulas for phase voltage RMS Squared and THD in PWM multiphase systems,‖ IEEE Trans. on Power Electron., vol. 30, no. 3, pp. 1645-1656, Mar. 2015.

[2]  A. F. Zobaa, ―Optimal multiobjective design of hybrid active power filters considering a distorted environment,‖ IEEE Trans. on Ind. Electron., vol. 61, no. 1, pp. 107-113, Jan. 2014.

[3]  X. Hao, X. Yang and T. Liu, "A sliding-mode controller with multiresonant sliding surface for single-phase grid connected VSI with an LCL Filter," IEEE Trans. on Power Electron., vol. 28, no. 5, pp. 2259-2268, May. 2013.

[4] Q. N. Trinh, and H. H. Lee, ―An advanced current control strategy for three phase shunt active power filters,‖ IEEE Trans. on Ind. Electron., vol. 60, no. 12, pp. 5400-5410, Dec. 2013.

[5] J. F. Petit, G. Robles, and H. Amaris, ―Current reference control for shunt active power filters under non sinusoidal voltage conditions, IEEE Trans. on Power Del., vol. 22, no.4, pp. 2254–2261, Oct. 2007.

Deadbeat Weighted Average CurrentControl with Corrective Feed-forward Compensation for Microgrid Converters with Non-Standard LCL Filter

ABSTRACT

 Microgrid converters are required to have the capability of both grid-tied mode and islanding mode operation. For this dual-mode operation, large shunt capacitors are often used in the interfacing converter output LCL filter, as it can help to stabilize supply voltage and to reduce switching ripple pollutions to sensitive loads during autonomous islanding operation. At the same time, this modification causes a few challenges, including the low frequency harmonic distortions, the steady-state tracking errors and the slow dynamic response, to the line current regulation during grid-tied operation. To overcome these drawbacks, a modified weighted average current controller is developed. First, to realize a fast line current response, a deadbeat control of weighted average current is developed based on a reduced-order virtual filter plant. Second, a grid voltage feed-forward term is added to the weighted average current reference to mitigate the steady-state line current tracking errors. Note that this compensation term is directly added to the current reference, thus, it is very well decoupled from the closed-loop current regulator. In addition, it can be seen that the low-order line current harmonics caused by grid voltage distortion is inherently compensated by this proposed corrective feed-forward control.

KEYWORDS:

1.      Virtual filter

2.      Deadbeat control

3.      Weighted average current control

4.      Active damping

5.      LCL filter

6.      Microgrid.

SOFTWARE: MATLAB/SIMULINK

CIRCUIT DIAGRAMS:

Fig. 1. Diagram of a grid-tied converter controlled by conventional weighted average current feedback.

Fig. 2. Diagram of the proposed control deadbeat scheme with weighted average current feedback and line current tracking error compensation.

EXPECTED SIMULATION RESULTS:

Fig.3. Performance of the system using the proposed deadbeat control method (compensation term is activated in 0.5sec). (from top to bottom: (1) grid voltage V_grid; (2) line current I₂ ; (3) output current I₁ ; (4) current tracking errors ( I_ref-I₂).)

Fig. 4. Performance of the system using the proposed deadbeat control method and the method in [14]. (from top to bottom: (1) grid voltageV_grid ; (2) line current I₂; (3) output current I₁ ; (4) current tracking errors ( ).)

Fig. 5. Performance of the system using the proposed method, operating in a distorted grid with grid impedance variation

Fig. 6. Performance of the system using the proposed deadbeat control method with feed-forward control. Grid frequency changes from 50Hz to 50.15Hz at 0.2sec. (from top to bottom: (1) Grid voltage V_grid; (2) line current I₂ ; (3) output current I₁; (4) weighted average current I₁₂ .)

Fig. 7. Performance of the system using the proposed deadbeat control method but without feed-forward control. Grid frequency changes from 50Hz to 50.15Hz at 0.2sec. (from top to bottom: (1) Grid voltage V_grid ; (2) line current I₂; (3) output current I₁; (4) weighted average current I₁₂ .)

Fig. 8. Performance of the system using the PI control for weighted average current regulation, with feed-forward control. Grid frequency changes from 50Hz to 50.15Hz at 0.2sec. (from top to bottom: (1) Grid voltage V_grid ; (2) line current I₂; (3) output current I₁; (4) weighted average current I₁₂.)

CONCLUSION

An enhanced current controller is proposed in this paper. The research work of this paper is summarized here as:

1) In order to realize rapid control of converter current, the deadbeat control is applied to regulate the weighted average current based on a virtual filter plant.

2) The feed-forward compensator is developed to mitigate the steady-state fundamental current tracking errors caused by conventional weighted average current control.

3) The frequency-selective capacitor leg current estimation is proposed and the corresponding compensation term can be used to increase the robustness of the converter against grid harmonic distortions. The design and implementation of this compensator are highly decoupled from the closed-loop deadbeat current regulator. Thus, both the current regulator and the compensator can be independently designed.

REFERENCES

[1]   F. Blaabjerg, Z. Chen, and S. B. Kjaer, ―Power electronics as efficient interface in dispersed power generation systems,‖ IEEE Trans. Power Electron., vol. 19, no. 5, pp. 1184-1194, May. 2004.

[2]   J. Rocabert, A. Luna, F. Blaabjerg, and P. Rodriguez, ―Control of power converters in AC microgrids,‖ IEEE Trans. Power Electron., vol. 27, no. 11, pp. 4734–4749, Nov. 2012.

[3]   Y. W. Li, D. M. Vilathgamuwa and P. C. Loh, ―Design, analysis and real-time testing of a controller for multibus microgrid system,‖ IEEE Trans. Power Electron., vol. 19, pp. 1195-1204, Sep. 2004.

[4]    J. M. Guerrero, L. G. Vicuna, J. Matas, M. Castilla, and J. Miret, ―A wireless controller to enhance dynamic performance of parallel inverters in distributed generation systems,‖ IEEE Trans. Power Electron., vol. 19, no. 4, pp. 1205-1213, Sep, 2004. 

Voltage Sag Mitigation Using Multilevel Inverter based Distribution Static Compensator (DSTATCOM) in Low Voltage Distribution System

 ABSTRACT

Among the different disturbances affecting the power quality, the voltage sag are considered as a most important power quality problem faced by utilities, industrial consumer & equipment like PLC (Programmable Logic Controller), ASD (Adjustable Speed Drives) which need to be fully investigated. Custom power device are effective means for mitigating the voltage related issues prominently voltage sag, unbalanced load voltage, voltage regulation, sag/ swell etc. by compensating the reactive power with the injection of shunt current. Various DSTATCOM topologies & control scheme are suggested in the literature. In this paper by using three level H-bridge topology & five level cascaded multilevel inverter based DSTATCOM the voltage sag is compensated effectively with reduced total harmonic distortion (THD).

KEYWORDS:

1.      Cascaded Multilevel Inverter

2.      DSTATCOM

3.      Power Quality

SOFTWARE: MATLAB/SIMULINK

CIRCUIT DIAGRAMS:

Fig. 1. Three-phase, 3-level H-bridge inverter based DSTATCOM

Fig. 2. Three-phase, 5-level Cascaded H-bridge inverter based DSTATCOM

BLOCK  DIAGRAM:

Fig. 3. System Block Diagram

EXPECTED SIMULATION RESULTS:

Fig. 4(a) Sag At Bus B3 (b) Injected Current By DSTATCOM (c) Compensated Voltage At Bus B3 (d)Active & Reactive Power At Bus B3 (e) Injected Active & Reactive (f) Compensated Active & Reactive Power at bus B3

Fig. 5 (a) Sag At Bus B3 (b) Injected Current By DSTATCOM (c) Compensated Voltage At Bus B3 (d)Active & Reactive Power At Bus B3 (e) Injected Active & Reactive (f) Compensated Active & Reactive Power at bus B3

Fig. 6(a) Phase voltage & Line voltage for 3-level inverter based DSTATCOM (b) Phase voltage & Line voltage for 5-level inverter based DSTATCOM

CONCLUSION

The paper presents the principle of operation of cascaded H-bridge converter and simulation studies on cascaded converter based DSTATCOM using Sinusoidal PWM control. It is observed that the DSTATCOM is capable of supplying the reactive power demanded by the load both during steady state and transient operating conditions. The harmonics in cascaded H-bridge five-level inverter current are less compared to three-level inverter operating at same switching frequency.

REFERENCES

[1]   M. H. J. Bollen, Understanding Power Quality Problems-Voltage Sags & Interruptions, New York, IEEE Press. 2000.

[2]    R. C. Duggan, F. Mc. Granaghan, H. Wayne Beaty, Electrical Power System Quality, McGraw-Hill. 1996.

[3]   Youn Soo-Young, Jung, Tae-Hyun Kim, Seung-II Moon & Byung- Moon Han. “Analysis and Control of DSTATCOM for Line Voltage Regulation” Power Engineering Society Winter Meeting, vol. 2, no. 2, pp. 726-734, Jan. 2002.

[4]    S. Iyer, A. Ghosh and A. Joshi, “Inverter Topologies for DSTATCOM applications-A Simulation Study,” Elect. Power Syst. Res., vol. 75, no.2/3, pp. 161-170, Aug. 2005.

[5]   C. A. Quinn, N. Mohan and H. Mehta, “Active Filtering of Harmonic Current in Three-Phase, Four-wire systems with Three-Phase and Single-Phase non-linear Loads,” Proc Appl. Power Electron. Conf., 1992, pp.829-836.