A Quasi-Resonant Switched-Capacitor Multilevel Inverter With Self-Voltage Balancing for Single-Phase High-Frequency AC Microgri

ABSTRACT:

In this paper, a quasi-resonant switched-capacitor (QRSC) multilevel inverter (MLI) is proposed with self-voltage balancing for single-phase high-frequency ac (HFAC) microgrids. It is composed of a QRSC circuit (QRSCC) in the frontend and an H-bridge circuit in the backend. The input voltage is divided averagely by the series-connected capacitors in QRSCC, and any voltage level can be obtained by increasing the capacitor number. The different operational mechanism and the resulting different application make up for the deficiency of the existing switched-capacitor topologies. The capacitors are connected in parallel partially or wholly when discharging to the load, thus the self-voltage balancing is realized without any high-frequency balancing algorithm. In other words, the proposed QRSC MLI is especially adapted for HFAC fields, where fundamental frequency modulation is preferred when considering the switching frequency and the resulting loss. The quasi-resonance technique is utilized to suppress the current spikes that emerge from the instantaneous parallel connection of the series-connected capacitors and the input source, decreasing the capacitance, increasing their lifetimes, and reducing the electromagnetic interference, simultaneously. The circuit analysis, power loss analysis, and comparisons with typical switched-capacitor topologies are presented. To evaluate the superior performances, a nine-level prototype is designed and implemented in both simulation and experiment, whose results confirm the feasibility of the proposed QRSC MLI.

KEYWORDS:

1.      High-frequency ac (HFAC) microgrids

2.      Quasi-resonant switched-capacitor (QRSC)

3.      Multilevel inverter (MLI)

4.      Self-voltage balancing

SOFTWARE: MATLAB/SIMULINK

BLOCK DIAGRAM:

 Fig. 1. Power sources for a single-phase 500-Hz microgrid.

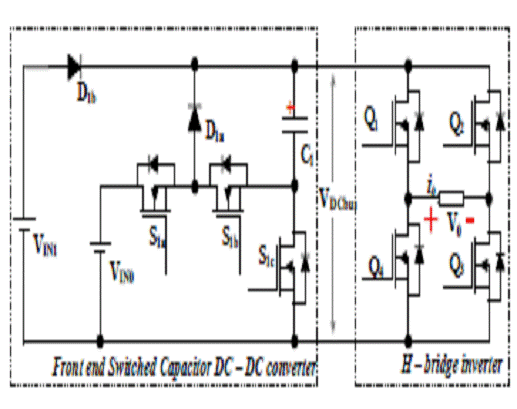
CIRCUIT DIAGRAM:

Fig. 2. Circuit of the proposed QRSC MLI when outputting 2n+1 levels.

EXPECTED SIMULATION RESULTS

Fig. 3. Simulation waveforms of the output voltages and currents under different load-types. (a) Vin = 100 V, fo = 500 Hz, ZL = 24 . (b) Vin = 100 V, fo = 500 Hz, ZL = 7.4+j11.3  (|ZL| = 13.5

Fig. 4. (a) Simulation waveforms of the voltages on capacitors C1~C4. (b) Simulation frequency spectrum of the staircase output.

Fig. 5. Simulation waveforms of the capacitors’ charging currents. (a) With quasi-resonant inductor. (b) Without quasi-resonant inductor.

CONCLUSION:

To make up for the deficiency that existing SC MLIs are inappropriate for the preferred series-connected input occasions like mode 2 in Fig. 1, a novel SC MLI is proposed in this paper with different structure and operational mechanism from the traditional ones, and to suppress the current spikes caused by the capacitors’ instant charging from the input source, a quasi-resonant inductor is embedded into the capacitors’ charging loop, reducing the EMI and longing the capacitors’ lifetimes. Meanwhile, the proposed QRSC MLI combines the advantages of the traditional SC MLI, such as self-voltage balancing under FFM and smaller voltage ripples for capacitors when used as HF power conversion, thus, especially adapted for HFAC microgrids.  The circuit configuration and the power loss analysis of the proposed QRSC MLI have been presented in this paper, as well as the comparisons with typical SC topologies. Lastly, a nine-level prototype is designed and implemented in both simulation and experiment. The results have validated the superior performances of the proposed topology.

REFERENCES:

[1] J. Drobnik, “High frequency alternating current power distribution,” Proceedings of IEEE INTELEC, pp. 292-296, 1994.

[2] S. Chakraborty, M. D. Weiss, and M. G. Simões, “Distributed intelligent energy management system for a single-phase high-frequency AC microgrid,” IEEE Trans. Ind. Electron., vol. 54, no. 1, pp. 97-109, Feb. 2007.

[3] S. Chakraborty and M. G. Simões, “Experimental evaluation of active filtering in a single-phase high-frequency AC microgrid,” IEEE Trans. Energy Convers., vol. 24, no. 3, pp. 673-682, Sept. 2009.

[4] S. B. Kjaer, J. K. Pedersen, and Frede Blaabjerg, “A review of single-phase grid-connected inverters for photovoltaic modules,” IEEE Trans. Ind. Appl., vol. 41, no. 5, pp. 1292–1306, Sep./Oct. 2005.

[5] J. Liu, K. W. E. Cheng, and J. Zeng, “A unified phase-shift modulation for optimized synchronization of parallel resonant inverters in high frequency power distribution system.” IEEE Trans. Ind. Electron., vol. 61, no. 7, pp. 3232,3247, Jul. 2014.

Development of a Proportional + Resonant (PR) Controller for a Three-Phase AC Micro-Grid Syst

ABSTRACT:

This document presents a Proportional + Resonant (PR) controller design for regulating the active and reactive power output of a three-phase AC Micro-Grid inverter system. The system employs a Voltage Sourced Inverter (VSI). The VSI is configured to operate as a current source through an interface L-filter. The power is controlled indirectly by controlling the inverter’s output current. The stationary reference frame strategy is adopted for the design of the PR controller. A model of a grid connected AC inverter and a detailed design of the inverter’s PR based control scheme are presented. The control scheme is developed and simulated in MATLAB/Simulink software environment. The control algorithm code is generated for a target device. Using Processor In-the Loop (PIL) simulation, functional equivalence testing is performed between the simulated control algorithm and the compiled algorithm code on the target device. Results in both normal and PIL simulations are discussed from the viewpoint of steady state and dynamic performance of the controller.

KEYWORDS:

1.      Stationary Reference Frame

2.      Processor In-the Loop

3.      Feedback Control

4.      Voltage Sourced Inverter

5.      Alpha-Beta transformation

6.      Proportional Resonant controller

SOFTWARE: MATLAB/SIMULINK

SCHEMATIC DIAGRAM:

Figure 1 Schematic diagram for a three-phase grid connected VSI

 EXPECTED SIMULATION RESULTS

Figure.2 Three-Phase grid voltages (Vabc)

Figure 3 Normal simulation α-axis current tracking due to a step change in Pref at t = 0.5s

Figure 4 Normal simulation system’s response tracking active power reference signal due to a step change in Pref at t = 0.5s

Figure 5 PIL simulation α-axis current tracking due to a step change in Pref at t = 0.5s

Figure 6 PIL simulation system’s response tracking active power reference signal due to a step change in Pref at t = 0.5s

CONCLUSION:

This paper has presented the effectiveness of using the Proportional Resonant (PR) control strategy to control active and/or reactive power transfer between the Micro-Grid and the transmission grid system. The PR controller tracks stationary frame reference currents calculated from the active (PC(t)) and reactive (QC(t)) PI controller actuating power outputs using d-q frame power equations. Consequently this improves the performance of the control loop as opposed to reference currents calculated directly from αβ frame power equations. The PR controller tracks reference currents with a very small steady-state error and reduced harmonic distortion. Model development and simulations were done using the MATLAB/Simulink software environment. Functional equivalence testing was performed between the simulated control algorithm and the compiled algorithm code on the real hardware target device. Same results were obtained for both normal and PIL simulation modes.

REFERENCES:

[1] A Yazdani and R Iravani, Voltage-Sourced Converters in Power Systems. New Jersey: John Wiley & Sons, Inc, 2010.

[2]  S. Meshram, G. Agnihotri, and S. Gupta, "A Modern Two DOF Controller for Grid Intergration with Solar Power Generator," International Journal of Electrical Engineering and Technology, vol. 3, no. 3, pp. 164-174, December 2012.

[3] X. Wang, J. M. Guerrero, F. Blaabjerg, and Z. Chen, "A Review of Power Electronics Based Microgrids," Journal of Power Electronics, vol. 12, no. 1, pp. 181-192, January 2012.

[4] J. J. V. Cardona, J. C. A. Gil; F. J. G. Sales, S. Segui-Chilet, S. O. Grau, and N. M. Galeano, "Improved Control of Current Controlled Grid Connected Inverters in Adjustable Speed Power Energies," Universidad Politecnica de Valencia and Universidad de Antioquia,.

[5] R. Teodorescu, M. Liserre, and P. Rodríguez, Grid Converters for Photovoltaic and Wind Power Systems.: John Wiley & Sons, Ltd, 2011.

Power management in PV-battery-hydro based standalone microgrid

ABSTRACT:

This work deals with the frequency regulation, voltage regulation, power management and load levelling of solar photovoltaic (PV)-battery-hydro based microgrid (MG). In this MG, the battery capacity is reduced as compared to a system, where the battery is directly connected to the DC bus of the voltage source converter (VSC). A bidirectional DC–DC converter connects the battery to the DC bus and it controls the charging and discharging current of the battery. It also regulates the DC bus voltage of VSC, frequency and voltage of MG. The proposed system manages the power flow of different sources like hydro and solar PV array. However, the load levelling is managed through the battery. The battery with VSC absorbs the sudden load changes, resulting in rapid regulation of DC link voltage, frequency and voltage of MG. Therefore, the system voltage and frequency regulation allows the active power balance along with the auxiliary services such as reactive power support, source current harmonics mitigation and voltage harmonics reduction at the point of common interconnection. The experimental results under various steady state and dynamic conditions, exhibit the excellent performance of the proposed system and validate the design and control of proposed MG.

SOFTWARE: MATLAB/SIMULINK

 CIRCUIT DIAGRAM:

Fig. 1 Microgrid Topology and MPPT Control

(a) Proposed PV-battery-hydro MG

 EXPECTED SIMULATION RESULTS

Fig. 2 Dynamic performance of PV-battery-hydro based MG following by solar irradiance change

(a) vsab, isc, iLc and ivscc, (b) Vdc, Ipv, Vb and Ib, (c) vsab, isa, iLa and ivsca, (d) Vdc, Ipv, Vb and Ib

Fig. 3 Dynamic performance of hydro-battery-PV based MG under load perturbation

(a) vsab, isc, Ipv and ivscc, (b) Vdc, Ipv, Vb and Ib, (c) vsab, isc, Ipv and ivscc, (d) Vdc, Ipv, and Vb

CONCLUSION:

In the proposed MG, an integration of hydro with the battery, compensates the intermittent nature of PV array. The proposed system uses the hydro, solar PV and battery energy to feed the voltage (Vdc), solar array current (Ipv), battery voltage (Vb) and battery current (Ib). When the load is increased, the load demand exceeds the hydro generated power, since SEIG operates in constant power mode condition. This system has the capability to adjust the dynamical power sharing among the different RES depending on the availability of renewable energy and load  demand. A bidirectional converter controller has been successful to maintain DC-link voltage and the battery charging and discharging currents. Experimental results have validated the design and  control of the proposed system and the feasibility of it for rural area electrification.

REFERENCES:

[1] Ellabban, O., Abu-Rub, H., Blaabjerg, F.: ‘Renewable energy resources: current status, future prospects and technology’, Renew. Sustain. Energy Rev.,2014, 39, pp. 748–764

[2] Bull, S.R.: ‘Renewable energy today and tomorrow’, Proc. IEEE, 2001, 89  (8), pp. 1216–1226

[3] Malik, S.M., Ai, X., Sun, Y., et al.: ‘Voltage and frequency control strategies of hybrid AC/DC microgrid: a review’, IET Renew. Power Gener., 2017, 11, (2), pp. 303–313

[4] Kusakana, K.: ‘Optimal scheduled power flow for distributed photovoltaic/ wind/diesel generators with battery storage system’, IET Renew. Power  Gener., 2015, 9, (8), pp. 916–924

[5] Askarzadeh, A.: ‘Solution for sizing a PV/diesel HPGS for isolated sites’, IET Renew. Power Gener., 2017, 11, (1), pp. 143–151

Phase Shifted Carrier Based Synchronized Sinusoidal PWM Techniques for Cascaded H-Bridge Multi Level Inverter

ABSTRACT:

This paper analyses synchronization strategy for cascaded H-Bridge multi level inverter (CHBMLI) topologies with carrier based sinusoidal phase shifted pulse width modulation (PSPWM) technique. In PSPWM technique a separate carrier is used for each H-Bridge (HB). The carriers are generally phase shifted from each other by π/x rad (x=No. of H-Bridges) for unipolar PWM. With the carrier frequency being an integer (odd/even) multiple of the fundamental frequency, it is observed that, the positions of zero crossings of the carriers with respect to the zero crossings of voltage references play an important role for maintaining quarter wave symmetry among multi level inverter (MLI) pole voltage waveforms. This paper analytically shows the conditions for half wave symmetry and quarter wave symmetry and experimentally verifies those conditions for PSPWM technique with a five level CHBMLI laboratory prototype.

KEYWORDS:

1.      Cascaded H-Bridge multilevel inverter

2.      Phase shifted carrier based PWM

3.      Synchronous PWM

4.      Half wave symmetry

5.      Quarter wave symmetry

SOFTWARE: MATLAB/SIMULINK

 CIRCUIT DIAGRAM:

Fig. 1. (a) Single H-Bridge ; (b) Double cascaded H-Bridges.

.

EXPECTED SIMULATION RESULTS

 Fig. 2. (a) and (d) Ch.1:-CHB1, Ch.2:-CHB2, Ch.3:-R1 and Ch.4:-R2; (b) and (e) Ch.1:-VHB1, Ch.2:-VHB2 and Ch.3:-VHB and (c) and (f) Ch.1:-VRO, Ch.2:- VBO and Ch.3:-VYO when (i) the zero crossings of voltage references are in phase with the zero crossings of carrier CHB1 and (ii) the zero crossings of voltage references are placed at the midpoint of the positive zero crossings of carriers CHB1 & CHB2 for fc=3fs with a modulation index of 0.8 and fs=50Hz.

Fig. 3. (a) and (d) Ch.1:-CHB1, Ch.2:-CHB2, Ch.3:-R1 and Ch.4:-R2; (b) and (e) Ch.1:-VHB1, Ch.2:-VHB2 and Ch.3:-VHB and (c) and (f) Ch.1:-VRO, Ch.2:- VBO and Ch.3:-VYO when (i) the zero crossings of voltage references are placed at +π/12rad with respect to the zero crossings of carrier CHB1 for fc=3fs with a modulation index of 0.8 and fs=50Hz and (ii) for fc=160Hz with a modulation index of 0.8 and fs=50Hz.

Fig. 4. (a) and (c) Ch.1:-VRO, Ch.2:-VYO, Ch.3:-VRY and Ch.4:-iR; (b) and (d) Harmonic spectrum of VRY for (i) the zero crossings of voltage references are in phase with the zero crossings of carrier CHB1 and (ii) the zero crossings of voltage references are placed at the midpoint of the positive zero crossings of carriers CHB1 & CHB2 for fc=3fs with a modulation index of 0.8 and fs=50Hz.

Fig. 5. (a) and (c) Ch.1:-VRO, Ch.2:-VYO, Ch.3:-VRY and Ch.4:-iR; (b) and (d) Harmonic spectrum of VRY for (i) the zero crossings of voltage references are placed at +π/12 rad with respect to the zero crossings of carrier CHB1 for fc=3fs and (ii) fc=160Hz with a modulation index of 0.8 and fs=50Hz.

Fig. 6. (a) Ch.2:- VHB1, Ch.3:- VHB2 and Ch.4:- VHB; (b) Harmonic spectrum of VRO; (c) Ch.1:-VRO, Ch.2:-VYO, Ch.3:-VRY and Ch.4:-iR and (d) Harmonic spectrum of VRY when the zero crossings of voltage references are in phase with the zero crossings of carrier CHB1 for fc=6fs with a modulation index of 0.8 and fs=50Hz.

Fig. 7. (a) Ch.2:- VHB1, Ch.3:- VHB2 and Ch.4:- VHB; (b) Harmonic spectrums of VRO; (c) Ch.1:-VRO, Ch.2:-VYO, Ch.3:-VRY and Ch.4:-iR and (d) Harmonic spectrums of VRY when the zero crossings of voltage references are placed at the midpoint of the zero crossings of carriers CHB1 & CHB2 for fc=6fs with a modulation index of 0.8 and fs=50Hz.

Fig. 8. (a) and (b) Ch.1:-CHB1, Ch.2:-CHB2, Ch.3:-R1 and Ch.4:-R2 and (c) and (d) Ch.1:-VHB1, Ch.2:-VHB2 and Ch.3:-VHB when (i) the zero crossings of voltage references are placed at the midpoint of the positive zero crossings of carriers CHB1 & CHB2 and (ii) the zero crossings of voltage references are in phase with the zero crossings of carrier CHB2 for fc=9fs with a modulation index of 0.9 and fs=45Hz.

Fig. 9. (a) Ch.1:-Transition signal,Ch.2:-CHB1,Ch.3:-CHB2 and Ch.4:-R-Phase voltage reference and (b) Ch.1:-Transition signal,Ch.2:-CHB1,Ch.3:-CHB2 and Ch.4:-iR during the transition from p=9 to p=3.

Fig. 10. (a) and (d) Ch.1:-VHB1, Ch.2:-VHB2, Ch.3:-VHB3 and Ch.4:-VHB4; (b) and (e) Ch.1:-VHB and (c) and (f) Harmonic spectrum of VHB when (i) the positive zero crossing of one carrier co-incides with the zero crossing of fundamental voltage reference and (ii) the zero crossing of fundamental voltage reference is placed at the midpoint of two adjacent carriers with a modulation index of 0.8, fs=50Hz and p=3 for a single phase nine level CHBMLI.

CONCLUSION:

This paper shows analytically the possible positions of zero crossings of the carriers with respect to the zero crossings of voltage references for the CHBMLIs using the PSPWM technique for maintaining three phase symmetry, half wave symmetry and quarter wave symmetry. Three phase and half wave symmetries are maintained among the H-Bridge pole voltage waveforms for any position of zero crossing of carrier with respect to the zero crossing of the voltage references, as long as carrier frequency is 3n time the fundamental frequency with n being any integer (even/odd). But the positions of zero crossings of the carriers with respect to the zero crossings of voltage references are important for maintaining quarter wave symmetry among the pole voltage waveforms. This is analytically studied in this paper for single and two cascaded H-Bridges and generalized for x number of cascaded H-Bridges. The study is experimentally verified with the help of a three phase five level CHBMLI laboratory prototype and the results are presented.

REFERENCES:

[1] J.Rodriguez; S.Bernet; Bin Wu; J.O.Pontt and S.Kouro, ―Multilevel Voltage-Source-Converter Topologies for Industrial Medium-Voltage Drives,‖ IEEE Transactions on Industrial Electronics , vol.54, no.6, pp.2930-2945, Dec. 2007.

[2] H.Abu-Rub; J.Holtz; J.Rodriguez and Ge Baoming, ―Medium-Voltage Multilevel Converters—State of the Art, Challenges, and Requirements in Industrial Applications,‖ IEEE Transactions on Industrial Electronics, vol.57, no.8, pp.2581-2596, Aug. 2010.

[3] S.Kouro; M.Malinowski; K.Gopakumar; J.Pou; L.G.Franquelo; Bin Wu; J.Rodriguez; M.A.Perez and J.L.Leonz   BB  B    , ―Recent Advances and Industrial Applications of Multilevel Converters,‖ IEEE Transactions on Industrial Electronics, vol.57, no.8, pp.2553-2580, Aug. 2010.

[4] G. Narayanan and V.T. Ranganathan, ―Two novel synchronized bus-clamping PWM strategies based on space vector approach for high power drives,‖ IEEE Trans.Power.Electron., vol.17, no.1, pp.84-93,Jan- 2002.

[5] A.R.Beig; S.Kanukollu.;K.Al Hosani and A.Dekka, ―Space-Vector-Based Synchronized Three-Level Discontinuous PWM for Medium-Voltage High-Power VSI‖, IEEE Transactions on Industrial Electronics, vol. 61,no.8,pp. 3891 – 3901, Aug. 2014.

Multi-Input Switched-Capacitor Multilevel Inverter for High-Frequency AC Power Distribution

 ABSTRACT:

This paper proposes a switched-capacitor multilevel inverter for high frequency AC power distribution systems. The proposed topology produces a staircase waveform with higher number of output levels employing fewer components compared to several existing switched capacitor multilevel inverters in the literature. This topology is beneficial where asymmetric DC voltage sources are available e.g. in case of renewable energy farms based AC microgrids and modern electric vehicles. Utilizing the available DC sources as inputs for a single inverter solves the major problem of connecting several inverters in parallel. Additionally, the need to stack voltage sources, like batteries or super-capacitors, in series which demand charge equalization algorithms, are eliminated as the voltage  sources employed share a common ground. The inverter inherently solves the problem of capacitor voltage balancing as each capacitor is charged to the value equal to one of input voltage every cycle. State analysis, losses and the selection of capacitance are examined. Simulation and experimental results at different distribution frequencies, power levels and output harmonic content are provided to demonstrate the feasibility of the proposed multilevel inverter topology.

KEYWORDS:

1.      H-bridge

2.      HFAC power distribution

3.      High frequency DC/AC Inverter

4.      Multilevel inverter

5.      Selective harmonic elimination

6.      Switched-capacitor

SOFTWARE: MATLAB/SIMULINK

CIRCUIT DIAGRAM:

Fig. 1: Proposed 7 level SCMLI topology

 EXPECTED SIMULATION RESULTS

Fig. 2: Simulation waveforms at 400 Hz including nonidealities

: (a) output voltage and current (b) switched capacitor

voltage and current

CONCLUSION:

A novel SCMLI topology for HFAC PDS has been proposed in this paper. The topology is applicable where unequal DC input sources are at disposal. Such scenarios are common in large renewable energy farms and electric vehicle networks. It is more convenient to employ multiple DC sources as input to a single inverter than to employ several inverters in parallel with their respective solitary DC input sources. This topology does not stack up the voltage sources in series and therefore does not require voltage balancing circuits. Since the switched capacitors employed copy the input voltage every cycle, the problem of voltage balancing has also been eliminated. The harmonic content in the waveform is analyzed and is found to be minimum. The proposed topology obtains higher number of voltage levels compared to several existing topologies. This paper utilizes the proposed topology for high frequency AC distribution. However, the same topology can be employed for 50 Hz / 60 Hz distribution by employing a larger switched capacitor. It is shown that the number of output voltage levels exponentially increase with increase in the employed input voltage sources and SCs. In the hardware results, it is shown that the 5th and 7th harmonics are minimized to very low value of 1V each. Results at different distribution frequencies and power levels are presented.

REFERENCES:

[1] Patel, Mukund R.,“High-Power High-Voltage Systems”, Spacecraft Power Systems, CRC press, 2004, ch. 22, sec. 22.7, pp. 539-543.

[2] Luk, Patrick Chi-Kwong, and Andy Seng Yim Ng. ”High Frequency AC Power Distribution Platforms.” Power Electronics in Smart Electrical Energy Networks. Springer London, 2008. pp. 175-201.

[3] Z. Ye, P. K. Jain and P. C. Sen, ”A Two-Stage Resonant Inverter With Control of the Phase Angle and Magnitude of the Output Voltage,” in IEEE Trans. Ind. Electron., vol. 54, no. 5, pp. 2797-2812, Oct. 2007.

[4] J. A. Sabate, M. M. Jovanovic, F. C. Lee and R. T. Gean, ”Analysis and design-optimization of LCC resonant inverter for high-frequency AC distributed power system,” in IEEE Trans. Ind. Electron., vol. 42, no. 1,pp. 63-71, Feb 1995.

[5] Status of 20 kHz Space Station Power Distribution Technology, NASA Publication, TM 100781.