A Hysteresis Current Controller for Grid-Connected Inverter with Reduced Losses

ABSTRACT:

In this paper, a hysteresis current controller with reduced losses for three-phase grid-connected inverter is proposed. In the proposed hysteresis current controller, one of the inverter phase is clamped to the positive or negative inverter buses depending on the polarity of the phase current. Totally, each inverter phase is clamped for the duration of one third of the fundamental output period. As the inverter phase is inactive when the current is the highest, the switching losses are reduced. Simulation and experimental results are included to show the effectiveness of the proposed controller.

KEYWORDS:

1.      Current controller

2.      Hysteresis

3.      Grid-connected inverter

4.      Losses

5.      Clamped

SOFTWARE: MATLAB/SIMULINK

 BLOCK DIAGRAM:

Fig.1. Power controller of grid-connected inverter

 EXPECTED SIMULATION RESULTS:

Fig.2. Output current and switching pattern of: (a) conventional hysteresis

current controller, (b) proposed hysteresis current controller

CONCLUSION:

A simple hysteresis current controller with reduced losses has been proposed in this paper. In the proposed current controller, one of the inverter phase is clamped to the positive or negative DC bus, depending on the polarity, when the magnitude of the current is the greatest. This lead to reduction of the average switching frequency as well as the switching losses. Simulation and experimental results have shown that the proposed hysteresis controller is able to reduce the switching losses without sacrificing the output current waveform.

REFERENCES:

[1] S. Jain and V. Agarwal, “A Single-Stage Grid Connected Inverter Topology for Solar PV Systems With Maximum Power Point Tracking,” IEEE Trans. Power Electron., vol. 22, no. 5, pp. 1928- 1940, 2007.

[2] M. Mohseni and S. M. Islam, “A new vector-based hysteresis current control scheme for three-phase PWM voltage-source inverters,” IEEE Trans. Power Electron., vol. 25, no. 9, pp. 2299– 2309, 2010.

[3] M. P. Kazmierkowski and M. A. Dzieniakowski, “Review of current regulation techniques for three-phase PWM inverters,” Proc. IECON’94 - 20th Annu. Conf. IEEE Ind. Electron., vol. 1, pp. 567– 575, 1994.

[4] Y. Zhang and H. Lin, “Simplified model predictive current control method of voltage-source inverter,” 8th Int. Conf. Power Electron. - ECCE Asia, pp. 1726–1733, 2011.

[5] C. C. Hua, C. W. Wu, and C. W. Chuang, “A digital predictive current control with improved sampled inductor current for cascaded inverters,” IEEE Trans. Ind. Electron., vol. 56, no. 5, pp. 1718–1726, 2009.

A Systematic Method for Designing a PR Controller and Active Damping of the LCL Filter for Single-Phase Grid-Connected PV Inverters

ABSTRACT:

 The Proportional Resonant (PR) current controller provides gains at a certain frequency (resonant frequency) and eliminates steady state errors. Therefore, the PR controller can be successfully applied to single grid-connected PV inverter current control. On the contrary, a PI controller has steady-state errors and limited disturbance rejection capability. Compared with the L- and LC filters, the LCL filter has excellent harmonic suppression capability, but the inherent resonant peak of the LCL filter may introduce instability in the whole system. Therefore, damping must be introduced to improve the control of the system. Considering the controller and the LCL filter active damping as a whole system makes the controller design method more complex. In fact, their frequency responses may affect each other. The traditional trial-and-error procedure is too time-consuming and the design process is inefficient. This paper provides a detailed analysis of the frequency response influence between the PR controller and the LCL filter regarded as a whole system. In addition, the paper presents a systematic method for designing controller parameters and the capacitor current feedback coefficient factor of LCL filter active-damping. The new method relies on meeting the stable margins of the system. Moreover, the paper also clarifies the impact of the grid on the inverter output current. Numerical simulation and a 3 kW laboratory setup assessed the feasibility and effectiveness of the proposed method.

KEYWORDS:

1.      Single phase

2.      Grid-connected

3.      LCL filter

4.      Active damping

5.      Proportional resonant (PR) controller

SOFTWARE: MATLAB/SIMULINK

CIRCUIT DIAGRAM:

Figure 1. Two-stage single-phase PV system with LCL-filter control scheme.

EXPECTED SIMULATION RESULTS:

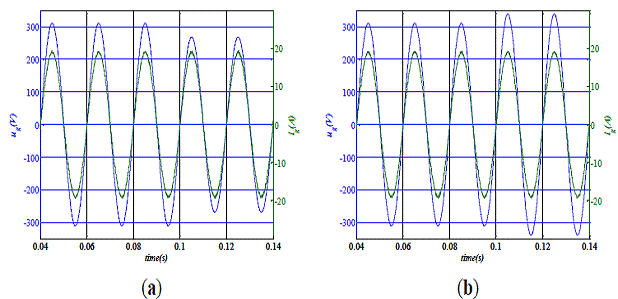
 Figure 2. Grid voltage and injected current at full load with nominal parameters: simulation results. (a) Grid voltage sag; (b) grid voltage swell.

Figure 3. Grid voltage and injected current at full load with inductor L1 variation: simulation results. (a) Inductor L1 increased by 20%: grid voltage sag; (b) Inductor L1 increased by 20%: grid voltage swell; (c) Inductor L1 decreased by 20%: grid voltage sag; (b) Inductor L1 decreased by 20%: grid voltage swell.

Figure 4. Grid voltage and injected current at full load with inductor L2 variation: simulation results. (a) Inductor L2 increased by 150%: grid voltage sag; (b) inductor L2 increased by 150%: grid voltage swell; (c) inductor L2 decreased by 20%: grid voltage sag; (b) inductor L2 decreased by 20%: grid voltage swell.

Figure 5. Grid voltage and injected current at full load with capacitor C variation: simulation results. (a) Capacitor C increased by 20%: grid voltage sag; (b) capacitor C increased by 20%: grid voltage swell; (c) capacitor C decreased by 20%: grid voltage sag; (b) capacitor C decreased by 20%: grid voltage swell.

 CONCLUSION:

The stability analysis of the system composed by a PR controller and an LCL filter together is not easy: the frequency responses may affect each other and the PR controller design becomes complex. The traditional method based on trial-and-error procedures, is too time-consuming, and the design process is inefficient. This paper provides a detailed analysis of the frequency response influence between the PR controller and the LCL filter. In addition, the paper presents a systematic design method for the PR controller parameters and the capacitor current feedback coefficient, used in the active damping of the LCL filter. Using the new parameters, a numerical simulation shows that the system meets the requirements of stable margins and current tracking steady-state error. The robustness of the current controller is verified through several experimental tests carried out on a 3 kW platform varying the system parameters. The Bode diagrams of the system varying inductor, capacitor, and grid impedance values confirmed that the controller parameters enhance robustness against the system parameters variation. Moreover, the system remains stable even in case of grid voltage fluctuation. Both the simulation and the experimental results assess the validity of the proposed design method.

REFERENCES:

1. Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galvan, E.; Guisado, R.C.P.; Prats, A.M.; Leon, J.I.; Moreno-Alfonso, N. Power-electronic systems for the grid integration of renewable energy sources: A survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016.

2. Wessels, C.; Dannehl, J.; Fuchs, F.W. Active Damping of LCL-Filter Resonance based on Virtual Resistor for PWM Rectifiers—Stability Analysis with Different Filter Parameters. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 3532–3538.

3. Castilla, M.; Miret, J.; Matas, J.; de Vicuna, L.G.; Guerrero, J.M. Control design guidelines for single-phase grid-connected photovoltaic inverters with damped resonant harmonic compensators. IEEE Trans. Ind. Electron. 2009, 56, 4492–4501.

4. Yi, L.; Zhengming, Z.; Fanbo, H.; Sizhao, L.; Lu, Y. An Improved Virtual Resistance Damping Method for Grid-Connected Inverters with LCL Filters. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition (ECCE 2011), Phoenix, AZ, USA, 17–22 September 2011; pp. 3816–3822.

5. Parker, S.G.; McGrath, B.P.; Holmes, D.G. Regions of Active Damping Control for LCL Filters. In Proceedings of the Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 53–60.

Single-Stage Buck-Derived LED Driver With Improved Efficiency and Power Factor Using Current Path Control Switches

ABSTRACT:

This paper proposes a single-stage light-emitting diode (LED) driver based on an inverted buck topology, using current path control switches. The proposed circuit consists of a control circuit, a bridge diode, and an inverted buck converter with multiple switches connected to the LED segments in parallel. Whereas the typical buck LED driver operates with a fixed LED forward voltage, the proposed driver operates with a variable LED forward voltage, according to the input voltage level. Because of this capability to adjust the LED forward voltage, it can reduce the current ripple and the switching frequency with a small inductance value. In addition, it enables operation with LED lamps of a wide voltage range, while simultaneously achieving small dead-angles. The detailed operation principles are described, and the design considerations for the proposed driver are discussed. The proposed driver circuit and control operation are verified experimentally using a 7 W hardware prototype with four LED segments. The obtained experimental results show that, under a 110 Vrms input voltage, the proposed driver achieves a power factor of 0.94 with a small dead-angle and an efficiency of 94 %.

KEYWORDS:        

                                                                                        

1.      Buck power factor collection (PFC)

2.      Constant off-time control

3.       Light-emitting diode (LED) driver

4.      Scalable LED string

SOFTWARE: MATLAB/SIMULINK

PROPOSED CIRCUIT DIAGRAM:

Fig. 1. Proposed single-stage LED driver..

 EXPECTED SIMULATION RESULTS:

Fig. 2. Simulation results for the proposed LED driver operated at

110Vrms/60 Hz. (a) Overall waveforms. (b) Switching waveforms at input peak

CONCLUSION:

This paper proposes an offline LED driver based on the inverted buck converter. The proposed driver is configured as a hybrid combination of buck topology and multiple switches, which connect to the several LED segments. The proposed driver can reduce both the switching frequency and the LED current ripple using relatively small inductors, because it can adjust the LED forward voltage according to the input voltage level. In addition, it has small dead-angles and achieves high efficiency values when used with high output voltages. The features and operation principles of the proposed LED driver have been described in detail. The overall schematic was presented, and its control method discussed. A 7 W prototype LED driver was implemented and tested. The obtained experimental results verify the operation and performance levels of the proposed driver. At 110 Vrms, it exhibits simultaneously a high efficiency (94 %) and a high PF value (0.94).

REFERENCES:

[1] T. Komine, and M. Nakagawa, “Fundamental analysis for visible-light communication system using LED lights,” IEEE Trans. Consumer Electron., vol. 50, no.1, pp.100-107, Jan. 2004.

[2] D. A. Steigerwald, J. C. Bhat, D. Collins, et al., “Illumination with solid state lighting technology,” IEEE Journal of Selected Topics in Quantum Electronics, vol. 8, no. 2, pp. 310–320, Mar. 2002.

[3] N. Narendran and Y. Gu, “Life of LED-based white light sources,” IEEE Display Technol., vol. 1, no. 1, pp. 167-151, Aug. 2005.

[4] T. Hao, J. Lam, and P. K. Jain, "A New High Power Factor, Soft-switched LED Driver without Electrolytic capacitors," in Proc. IEEE APEC, 2013, pp.823-828.

[5] Y. Y Hsieh, and Y. Z. Juang, “Analysis and Suppression of Over current in Boost LED Drivers,” IEEE Display Technol., vol. 9, no. 5, pp. 388-395, May 2013.

A Hybrid PV-Wind-Diesel System for Optimal Performance in Microgrid

ABSTRACT:  

The PV-Hydro Diesel technology can be made attractive option because the features various merits like as low maintenance requirement, environmental friendliness and absence of fuel cost. The efficiency of energy conversion a PV generation system may low because sun power cell exhibits to the nonlinear voltage and current and power versus voltage characteristics. The recent advancements in the technology and the reduction of fossil fuel resources have further contributed to the cause. But still, there lies several challenges to it. The paper proposes a novel approach of hybridization of renewable sources using Maximum Peak Power Transfer technique and optimal control. The performance of our approach is quite better than its other counterparts in terms of transient state and the magnitude of voltage obtained.

KEYWORDS:

1.      MPPT

2.      PV- Hydro - Diesel

3.      Perturb and observe

 SOFTWARE: MATLAB/SIMULINK

 PROPOSED MODEL:

Fig. 1: Representing the overall proposed model

 EXPECTED SIMULATION RESULTS:

Fig. 2 Representing The FFT analysis of the voltage waveform at the load end. when the FFT analysis of the wave form is done the THD value is found to be 0.17 %.

Fig.3: The THD of the output

CONCLUSION:

This paper proposed a novel approach of utilising a New Hybrid Technique approach to solve the MPPT problem in microgrid consisting of PV-Hydro Diesel cell connected to a grid using three phase inverter. The solar cell model was designed and given to boost converter. The converter output was analysed. An incremental conductance technique was also implemented for comparison purpose. The result of hybrid model was found to be quite better than the incremental conductance technique in terms of output voltage magnitude and THD content. The THD content reduces using our proposed approach. Also when the current is compared, the oscillations die out very fast in case of hybrid model while in I&C approach it is more or less sustained. In future this algorithm can be improved using other techniques and approaches. Also real time implementation of the algorithms can be done and hardware testing can be done. Hybrid with other algorithms can be utilised and the performances can be compared. Also clustering and other gradient learning methods can be utilised and the model can be tested for grid connection.

REFERENCES:

[1] Reddy, K. Pavankumar, and M. Venu Gopala Rao. "Modelling and Simulation of Hybrid Wind Solar Energy System using MPPT." Indian Journal of Science and Technology 8, no. 23 (2015).

[2] Dalala, Zakariya M., Zaka Ullah Zahid, Wensong Yu, Younghoon Cho, and Jih-Sheng Lai. "Design and analysis of an MPPT technique for small-scale wind energy conversion systems." Energy Conversion, IEEE Transactions on 28, no. 3 (2013): 756-767.

[3] Jain, S., Agarwal, V., 2004. A new algorithm for rapid tracking of approximate maximum power point in PV-Hydro systems. IEEE Trans. Power Electron. 2, 16–19.

[4] Bhandari, Binayak, Shiva Raj Poudel, Kyung-Tae Lee, and Sung-Hoon Ahn. "Mathematical modeling of hybrid renewable energy system: A review on small hydro-solar-wind power generation." international journal of precision engineering and manufacturing-green technology 1, no. 2 (2014): 157-173.

[5] S. Yuvarajan and JulineShoeb, “A Fast and Accurate Maximum Power Point Tracker for PV Systems,” IEEE, 2008.

Solar Photovoltaic Array Fed Luo Converter BasedBLDC Motor Driven Water Pumping System

 ABSTRACT:  

This paper deals with the solar photovoltaic (SPV) array fed water- pumping system using a Luo converter as an intermediate DC-DC converter and a permanent magnet brushless DC (BLDC) motor to drive a centrifugal water pump. Among the different types of DC-DC converters, an elementary Luo converter is selected in order to extract the maximum power available from the SPV array and for safe starting of BLDC motor. The elementary Luo converter with reduced components and single semiconductor switch has inherent features of reducing the ripples in its output current and possessing a boundless region for maximum power point tracking (MPPT). The electronically commutated BLDC motor is used with a voltage source inverter (VSI) operated at fundamental frequency switching thus avoiding the high frequency switching losses resulting in a high efficiency of the system. The SPV array is designed such that the power at rated DC voltage is supplied to the BLDC motor-pump under standard test condition and maximum switch utilization of Luo converter is achieved which results in efficiency improvement of the converter. Performances at various operating conditions such as starting, dynamic and steady state behavior are analyzed and suitability of the proposed system is demonstrated using MATLAB/Simulink based simulation results. 

KEYWORDS:

1.      SPV array

2.      Luo converter

3.      BLDC motor

4.      Centrifugal water pump

5.      MPPT

6.      Switch utilization

SOFTWARE: MATLAB/SIMULINK

BLOCK DIAGRAM:

Fig. 1 Configuration of proposed SPV array-Luo converter fed BLDC motor drive for water pumping system.

EXPECTED SIMULATION RESULTS:

Fig. 2 Performances of SPV array of the proposed SPV array-Luo converter

fed BLDC motor drive for water pumping system.

Fig. 3 Performances of Luo converter of the proposed SPV array-Luo

converter fed BLDC motor drive for water pumping system.

Fig. 4 Performances of BLDC motor-pump of the proposed SPV array-Luo

converter fed BLDC motor drive for water pumping system.

CONCLUSION:

A solar photovoltaic array fed Luo converter based BLDC motor has been proposed to drive water-pumping system. The proposed system has been designed, modeled and simulated using MATLAB along with its Simulink and sim-power system toolboxes. Simulated results have demonstrated the suitability of proposed water pumping system. SPV array has been properly sized such that system performance is not influenced by the variation in atmospheric conditions and the associated losses and maximum switch utilization of Luo converter is achieved. Luo converter has been operated in CCM in order to reduce the stress on power devices. Operating the VSI in 120° conduction mode with fundamental frequency switching eliminates the losses caused by high frequency switching operation. Stable operation of motor pump system and safe starting of BLDC motor are other important features of the proposed system.

REFERENCES:

[1] Fei Ding, Peng Li, Bibin Huang, Fei Gao, Chengdi Ding and Chengshan Wang, “Modeling and simulation of grid-connected hybrid photovoltaic/battery distributed generation system,” in China Int. Conf. Electricity Distribution (CICED), 13-16 Sept. 2010, pp.1-10.

[2] Zhou Xuesong, Song Daichun, Ma Youjie and Cheng Deshu, “The simulation and design for MPPT of PV System Based on Incremental Conductance Method,” in WASE Int. Conf. Information Eng. (ICIE), vol.2, 14-15 Aug. 2010, pp.314-317.

[3] B. Subudhi and R. Pradhan, “A Comparative Study on Maximum Power Point Tracking Techniques for Photovoltaic Power Systems,” IEEE Trans. Sustainable Energ., vol. 4, no. 1, pp. 89-98, Jan. 2013.

[4] M. A. Eltawil and Z. Zhao, “MPPT techniques for photovoltaic applications,” Renewable and Sustainable Energy Reviews, vol. 25, pp. 793-813, Sept. 2013.