Frequency Adaptive Fractional Order Repetitive Control of Shunt Active Power Filters

ABSTRACT:

Repetitive control which can achieve zero steady-state error tracking of any periodic signal with known integer period, offers active power filters a promising accurate current control scheme to compensate the harmonic distortion caused by nonlinear loads. However, classical repetitive control cannot exactly compensate periodic signals of variable frequency, and would lead to significant performance degradation of active power filters. In this paper a fractional order repetitive control strategy at fixed sampling rate is proposed to deal with any periodic signal of variable frequency, where a Lagrange interpolation based fractional delay filter is used to approximate the factional delay items. The synthesis and analysis of fractional-order repetitive control systems are also presented. The proposed fractional-order repetitive control offers fast on-line tuning of the fractional delay and the fast update of the coefficients, and then provides active power filters with a simple but very accurate real-time frequency adaptive control solution to the elimination of harmonic distortions under grid frequency variations. A case study of single-phase shunt active power filter is conducted. Experimental results are provided to demonstrate the validity of the proposed fractional-order repetitive control.

KEYWORDS:

1.      Active power filter

2.      Fractional order

3.       Repetitive control

4.      Frequency variation

SOFTWARE: MATLAB/SIMULINK

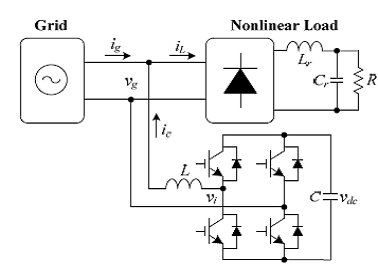
CIRCUIT DIAGRAM:

Fig. 1. Single-phase shunt APF connected to the grid with nonlinear load.

CONTROL SYSTEM

Fig. 2. Dual-loop control scheme for single-phase APF.

  EXPECTED SIMULATION RESULTS:

             

Fig. 3. Steady-state responses at 50Hz without APF: (a) grid voltage v_g and grid current i_g, (b) harmonic spectrum of v_g, (c) harmonic spectrum of i_g.

Fig. 5. Steady-state responses at 50Hz with CRC controlled APF: (a) grid voltage v_g and grid current i_g, (b) harmonic spectrum of compensated i_g.

Fig. 4. Steady-state responses at 49.8Hz with CRC controlled APF: (a) grid voltage v_g and grid current i_g, (b) compensation current i_c, reference current i_ref and current tracking error, (c) harmonic spectrum of i_g.

Fig. 5. Steady-state responses at 49.8Hz with FORC controlled APF: (a) grid voltage v_g and grid current i_g, (b) compensation current i_c, reference current i_ref and current tracking error, (c) harmonic spectrum of i_g.

Fig. 6. Steady-state responses at 50.2Hz with CRC controlled APF: (a) grid voltage v_g and grid current i_g, (b) compensation current i_c, reference current i_ref and current tracking error, (c) harmonic spectrum of i_g.

Fig. 7. Steady-state responses at 50.2Hz with CRC controlled APF: (a) grid voltage v_g and grid current i_g, (b) compensation current i_c, reference current i_ref and current tracking error, (c) harmonic spectrum of i_g.

Fig. 8. Responses to step changes of grid frequency: (a) 49.5Hz→50.5Hz, (b)

50.5Hz→49.5Hz.

Fig. 9. Responses to step load changes at 49.8Hz fundamental frequency: (a) R 15Ω→30Ω, (b) R 30Ω→15Ω.

CONCLUSION:

This paper proposes a frequency adaptive FORC scheme with fixed sampling rate to track or eliminate any periodic signal with variable frequency. Using Lagrange interpolation based FD filter to approximate the fractional delay items in RC, the proposed FORC offers fast on-line tuning of the fractional delay and the fast update of the coefficients. It provides APFs with a simple but very accurate real-time frequency adaptive control solution to harmonics distortions compensation under grid frequency variations. The stability criteria of FORC systems are given, which are compatible with those of CRC systems. A study case of FORC based single-phase shunt APF is done. Experiment results show the effectiveness of the proposed FORC strategy. Furthermore, the Lagrange interpolation based FORC can be used in extensive applications, such as the feeding currents control of grid connected converters [10]-[11], [27], programmable AC power supply [28], active noise cancelation, and so on.

REFERENCES:

[1] H. Akagi, “New trends in active filters for power conditioning,” IEEE Trans. Ind. Applicat., vol. 32, no. 6, pp. 1312-1322, Nov./Dec. 1996.

[2] H. Akagi, “Active harmonic filters,” Proceedings of the IEEE, vol. 93, no. 12, pp. 2128-2141, Dec. 2005.

[3] Y. Han, L. Xu, M. M. Khan, C. Chen, G. Yao, and L. Zhou, “Robust deadbeat control scheme for a hybrid APF with resetting filter and ADALINE-based harmonic estimation algorithm,” IEEE Trans. Ind. Electron., vol. 58, no. 9, pp. 3893-3904, Sep. 2011.

[4] M. Angulo, D. A. Ruiz-Caballero, J. Lago, M. L. Heldwein, and S. A. Mussa, “Active power filter control strategy with implicit closed-loop current control and resonant controller,” IEEE Trans. Ind. Electron., vol. 60, no. 7, pp. 2721-2730, Jul. 2013.

[5] P. Mattavelli and F. P. Marafao, “Repetitive-based control for selective harmonic compensation in active power filters,” IEEE Trans. Ind. Electron., vol. 51, no. 5, pp. 1018-1024, Oct. 2004.